Birthday ExampleThe Birthday attack equation determines the probability of two people having the same birthday given n people. The results are then:
Try an example
TheoryTo understand the birthday attack, let us start with the probability that one person will not have the same birthday as themselves: P(no match) = 365/365 For two people, we have 364 days to choose from, so the probably that they will not have the sample birthday is: P(no match) = 365/365 x 364/365 Then for three people we only have 363 days left often after checking the first two people to give: P(no match) = 365/365 x 364/365 x 363/365 If we have n people, then we can then write this as: 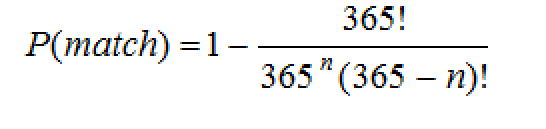
We use this in computer security to find collisions in hash signatures. With hash values we can find a collision using the birthday problem. It defines that we take a set of n randomly chosen people, and there will be a certain percentage that will have the same birthday. A group size of only 70 people results in a 99.9% chance of two people sharing the same birthday. Using this method, if we take an m-bit output there are 2^m messages, and the same hash value would only require 2^(m/2) random messages Blog: [Here] Sample code
public string birth(double val1, double val2)
{
double counter = val1;
double res = 1;
for (int i = 0; i < ((int)val1 - (int)(val1 - val2)); i++)
{
res = res * counter;
counter = counter - 1;
}
res = 1 - (res / (double)Math.Pow((double)val1, (double)val2));
return (String.Format("{0:0.00}%", 100 * res));
}
| |||