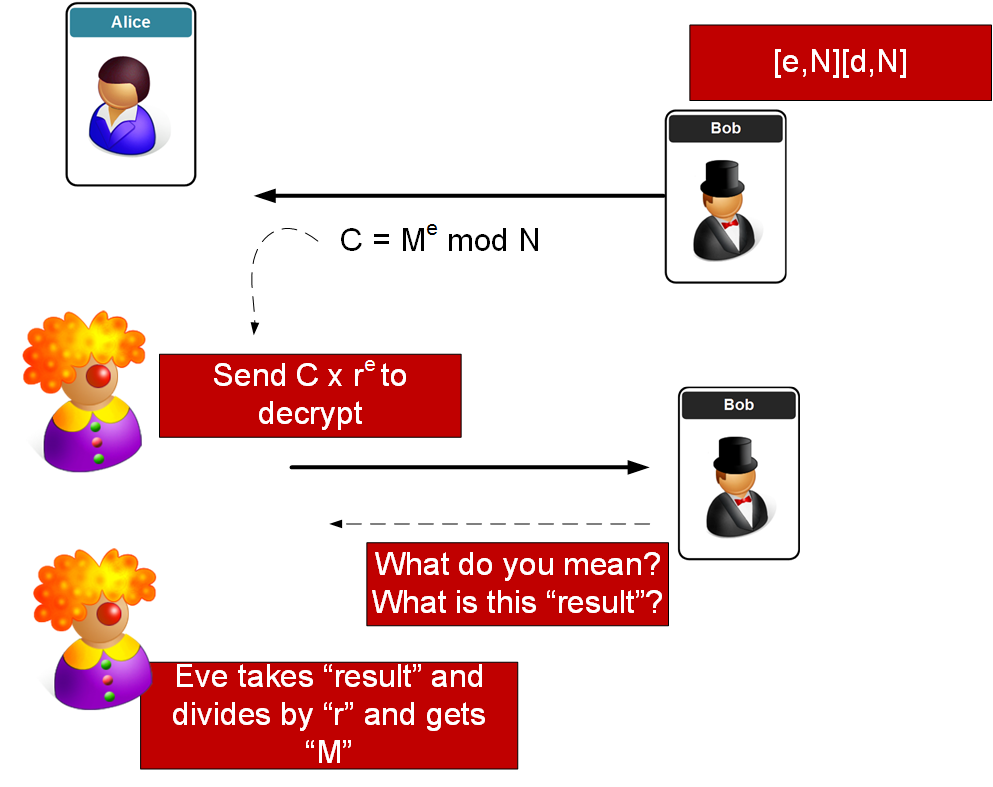
In this attack Eve gets Bob to cipher a chosen ciphertext. First Eve captures some cipher text, and then sends this back (with a random value raised to the power of Bob's encryption key (e)) and if Eve can determine the decrypted value, she can crack the message:
Chosen Cipher Attack |
Outline
First Eve listens for a cipher that she want to crack:
\(C = M^e \pmod N\)
Next she takes this cipher and gets Bob to decrypt it (and also multiplying by a random value to the power of Bob's e value):
\(C' = C \times r^e \pmod N\)
If Eve can determine the decrypted value for this cipher, she can determine the message as:
\( (C')^d = (C \times r^e)^d = (M^e \times r^e)^d = M^{e \times d} \times r^{e \times d} = M \times r\)
as \((M^e)^d \pmod N\) must equal \(M^1 \pmod N\)
So Eve just takes the original cipher, and divides it by the random value (r).
Here is the method:
Coding
An outline of the code is:
print '==Initial values ====' print 'e=',e,'d=',d,'N=',N print 'message=',M,'r=',r print '\n============='
Key calculation
Let’s select:
P=47 Q=71
The calculation of n and PHI is:
n=P × Q = 13 × 11 = 3337 PHI = (p-1)(q-1) = 3220
We can select e as:
e = 79
Next we can calculate d from:
(79 × d) mod 3220 = 1 [Link] d = 1019 Encryption key [3337,79] Decryption key [3337,1019]
Then, with a message of 688, we get:
\(Cipher = (688)^{79} \pmod {3337} = 1570\)
\(Decoded = (1570)^{1019} \pmod {3337} = 688\)