With Zero-knowledge proof, we ask Peggy to show that she knows the Hamiltonian cycle for a graph:
Zero-knowledge proof (Graphs) |
Method
Now we have a complex maze in front of us, and I want to know if you know the secret way through the maze, but others are listening, so how do I make sure you know?
This is a common problem in zero-knowledge proofs. In this case Peggy wants to make sure that Victor knows the secret (the way though the maze), but does not him to reveal it. For this we have a Hamiltonian cycle - which is the route through a maze which returns to the same point, and where we visit each of the nodes on the graph. If the maze is complex, it will be difficult for Eve to find the Hamiltonian cycle.
As an example let's take an extremely simple maze:
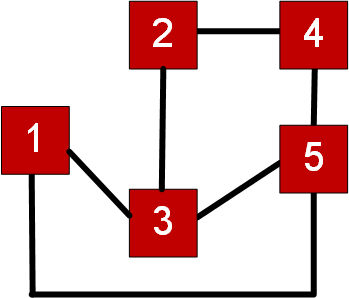
We could walk from 1 to 3 to 5 and then back to 1, but we have missed out 2 and 3. So what is a solution for us to be able to visit each junction (vertice) just one. In this case the Hamiltonian cycle will be 1 -> 5 -> 4 -> 2 -> 3 -> 1, and which return as back to 1, and having visited all the vertices in the maze.
In this case we have 10 Hamiltonian cycle routes, with two which will return to the starting point (1):
1 -> 5 -> 4 -> 2 -> 3 -> 1 1 -> 3 -> 2 -> 4 -> 5 -> 1 3 -> 2 -> 4 -> 5 -> 1 -> 3 3 -> 1 -> 5 -> 4 -> 2 -> 3 2 -> 4 -> 5 -> 1 -> 3 -> 2 2 -> 3 -> 1 -> 5 -> 4 -> 2 5 -> 4 -> 2 -> 3 -> 1 -> 5 5 -> 1 -> 3 -> 2 -> 4 -> 5 4 -> 5 -> 1 -> 3 -> 2 -> 4 4 -> 2 -> 3 -> 1 -> 5 -> 4
We have 12 Hamiltonian paths - which are routes where we go to every node, but don't have to end at the same one:
1 -> 5 -> 4 -> 2 -> 3 1 -> 3 -> 5 -> 4 -> 2 1 -> 3 -> 2 -> 4 -> 5 3 -> 2 -> 4 -> 5 -> 1 3 -> 1 -> 5 -> 4 -> 2 2 -> 4 -> 5 -> 1 -> 3 2 -> 3 -> 1 -> 5 -> 4 5 -> 4 -> 2 -> 3 -> 1 5 -> 1 -> 3 -> 2 -> 4 4 -> 2 -> 3 -> 5 -> 1 4 -> 5 -> 1 -> 3 -> 2 4 -> 2 -> 3 -> 1 -> 5
While this looks simple; for a complex graph, it is computationally infeasible to find the Hamiltonian cycle as it is a know as NP-complete. Peggy just has to show to Victor that she knows the Hamiltonian cycle, and then Victor will know that she knows the secret.So let's goBoth Peggy and Victor know the original graph (G), and Peggy knows the Hamiltonian cycle. Peggy then recreates the graph (H), but with different names for the nodes (vertices). As the graphs are the same in their structure, Peggy will easily be able to translate between the two graphs:
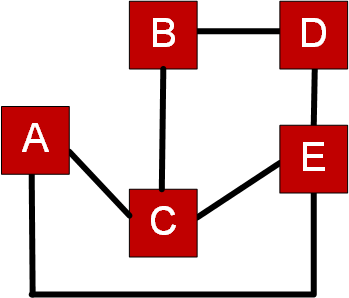
Now, it's the same structure for the graph, so Peggy will be able to find the Hamiltonian cycles, but others will have to search for them, and which is a difficult problem for a complex graph.
Victor will then ask Peggy some questions. He can either ask her to show how she converted from G to H, or reveal a Hamiltonian cycle in H. If she reveals the Hamiltonian cycle, she will show the translation (the route) for it to Victor.
This solution is an example of the travelling salesman problem (TSP) where a salesman must visit each city and where they must visit each city just once, and return to the same city they started from, and is known to be a NP-complete problem. In this way we have a puzzle which is easy for Peggy to solve, but Eve will find it difficult with a new graph each time.
So, increasingly we will see puzzles appearing, and which aim to be easy to solve if you are how you say you are, but difficult - if not near impossible - if you are not.
Code
Here's the outine code for graphing:
import matplotlib.pyplot as plt
import networkx as nx
graph = {'1': ['3','5'],
'2': ['3', '4'],
'3': ['2','1','5'],
'4': ['2','5'],
'5': ['1','4']}
file1='1111'
Graphnew=nx.Graph()
Graphnew.add_nodes_from(graph)
Gr=graph
for i in Gr:
for j in Gr[i]:
Graphnew.add_edge(i,j)
# print (str(i),',',str(j))
nx.draw(Graphnew,node_color='b',font_size=18,font_color='w',node_size=1000,with_labels=True)
f2= file1+".png"
plt.savefig(f2,format='PNG')