In this case we will determine the cyclic group G of order p and with a generator g:
Picking g value in ElGamal and discrete logs |
Outline
In reading about cryptography, have you ever come across the term of a cyclic group G of order p and with a generator g? This article will hopefully explain what this means.
The world of public key encryption is currently dominated by two things: discrete logarithms and elliptic curve methods. RSA is becoming a thing of the past for new applications, but it is only hanging on as it has such a monopoly in digital certificates. And so with discrete logarithms and the Diffie-Hellman method we end up with:
\(Y = g^x \pmod p\)
where we have a generator value (g) and a prime number p. The challenge is that even though we know Y, g and p, it is extremely difficult to determine the x value if we use a large prime number.
So can we use any value of g, and should it be as large as possible? The answer to both of these questions is no. If select a prime number of 7, and then select g values of 2, 3, 4 …9, and then calculate the results we get [spreadsheet]:
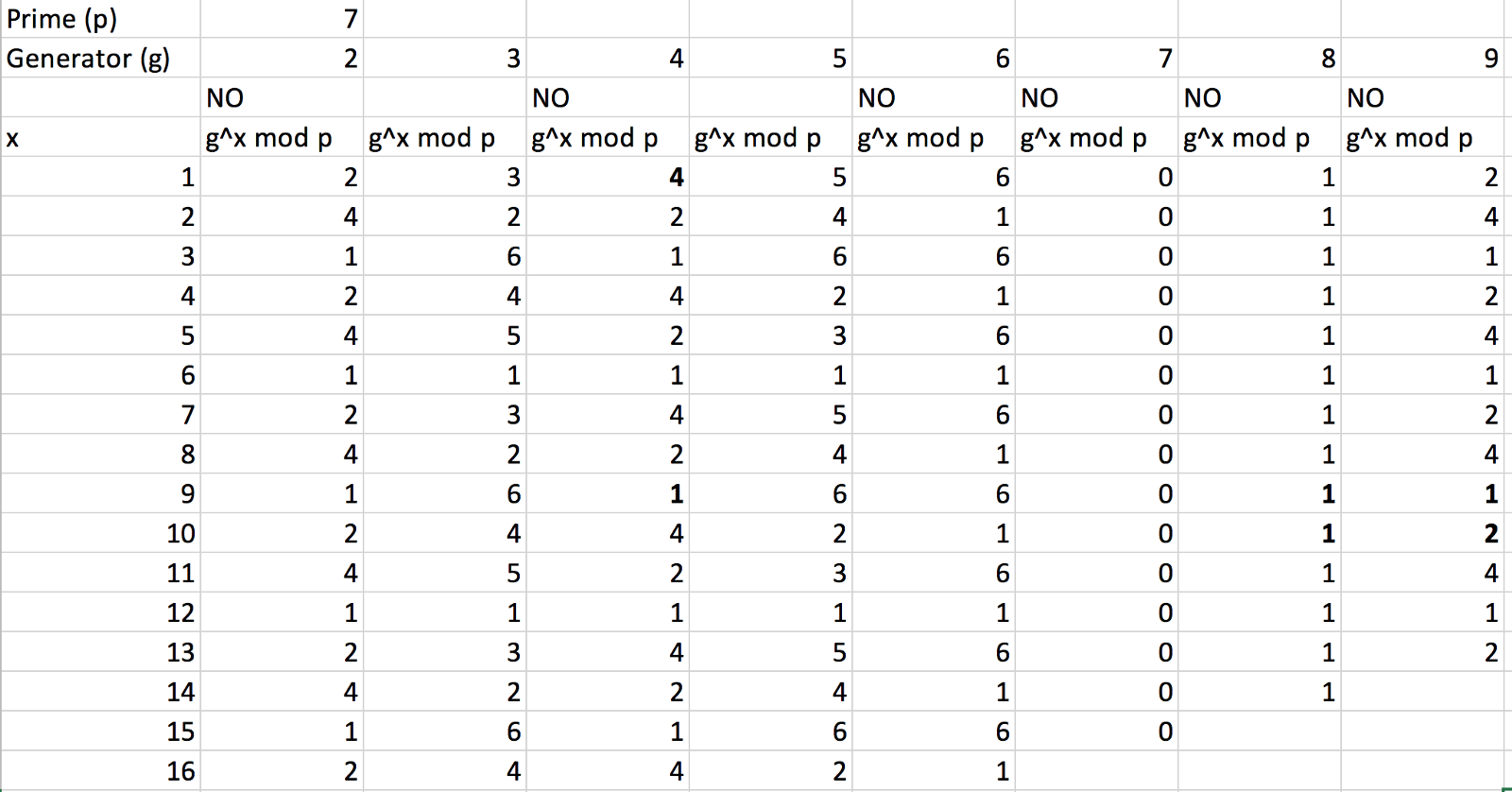
Now look at g=2, we get an output of 2, 4, 1, 2, 4 … for the sequence values of 1, 2, … This means that we do not get a unique output for the values from 1 to 6(where the maximum value will be six as we take the modulus of 7). But look at g=3, we get 3 (3¹ mod 7), 2 (3² mod 7), 6 (3³ mod 7), 4 (3⁴ mod 7), 5 (3⁵ mod 7), and 1 (3⁶ mod 7), which means that we get a unique value for all the possible outputs from 1 to 6, and which then repeats. For a prime number of 7, the valid values of g are 3 and 5.
But, in order to demonstrate the principle, I have done this is a long-handed way, so how do I find out all the possible values of G for a given prime number (p)? Well here’s a nice simple method in Python that I created to test up to p):
p=11
def getG(p):
for x in range (1,p):
rand = x
exp=1
next = rand % p
while (next != 1 ):
next = (next*rand) % p
exp = exp+1
if (exp==p-1):
print (rand,end=' ')
print ("p: ",p)
print ("Values for g^x mod p: ")
print (getG(p))
print getG(p)
Presentation
The following is an outline: