Is your number really random?

You won’t believe the number of code reviews that I have done, where I had to point out that the keys that were being generated were not…

Is your number really random?

You won’t believe the number of code reviews that I have done, where I had to point out that the keys that were being generated were not actually random, and would always be created in a predictable way.

The usage of random numbers can cause many problems, as developers often just link to standard libraries which do not quite generate a proper random number, or which repeat in every time they are called.

Within cryptography, random numbers are used to generate things like encryption keys. If the generation of these keys could be predicted in some way, it may be possible to guess them. The two main types of random number generators are:

Pseudo-Random Number Generators (PRNGs). This method repeats the random numbers after a given time (periodic). They are fast and are also deterministic, and are useful in producing a repeatable set of random numbers.
True Random Number Generators (TRNGs). This method generates a true random number and uses some which is random. One approach is to monitor the movements of a mouse pointer on a screen or from the pauses in key-strokes. Overall the method is generally slow, especially if it involves human interaction, but is non-deterministic and aperiodic.

Normally simulation and modelling applications use PRNG, so that the values generated can be repeated for different runs, while cryptography, lotteries, gambling and games use TRNG, as each value which is selected at random should not repeat or be predictable. Eve could thus guess the key created by the method that Bob uses to generate a key. So, in the generation of encryption keys for public-key encryption, user’s are typically asked to generate some random activity. The random number is then generated based on this activity.

Computer programs, though, often struggle to generate TRNG, and hard-ware generators are often used within highly secure applications. One method is to generate a random number based on low-level, statistically random “noise” signals. This includes things like thermal noise and from the photoelectric effect.

Within cryptography, it is important that we are generating values which are as near random, so that Eve cannot guess the random numbers that Bob and Alice are used. With randomness, we cannot determine how random the values are by just taking a few samples. For this, we need a large number of samples and make an estimation of the overall randomness.

There are various tests for randomness. For example, we could define an aver-age value which is halfway between the number range, and then determine the ratio of the values above and below the halfway value. This will work, but will not show us if the values are well distributed. Along with this we could determine the arithmetic mean of the values, and match it to the centre value within the range of numbers. An improved method to test for the distribution of values is the Monte Carlo value for Pi test. With this method, we take our random numbers and scale them between 0.0 and 1.0. Next, we take two values at a time and calculate:

Sqrt(x² + y²)

If this value is less than or equal to one, we place in the circle (with a radius of 1), otherwise, it is out of the circle. The estimation of PI is then four times the number of points in the circle (M) divided by the total number of points (N). In the figure below, the blue points are outside the circle and the yellow ones are inside:

We thus need to test our data and see if we get a value close to PI.

Here is a sample run with 10 values [here] that are generated from random.org:

First Five Pairs:
 X Y Z:
 -0.671 -0.098 0.678
 -0.6 -0.553 0.816
 0.616 0.867 1.063
 -0.678 0.09 0.684
 -0.569 0.443 0.721

Inval: 4 Outval: 1

Result: 3.2
 — — — — — — — — 
Values Used: [42, 115, 51, 57, 206, 238, 41, 139, 55, 184]

A value of 3.2 is close to PI (3.14), so we have a good set of random values. If you would like to try other ones, try here.

Entropy

Another method for determining randomness is to measure the entropy of the data. It is defined by Claude E. Shannon in his 1948 paper, where the maximum entropy occurs when there is an equal distribution of all bytes across the data. Normally we define these in terms of bytes. The method we use is to take the frequencies of the byte values and calculate how many bits are at used. A maximum entropy is 8 bits (for a byte value):

Here is the calculator is here.

Linear Congruential Random Number Generator

One method of creating a simple random number generator is to use a sequence generator of the form:

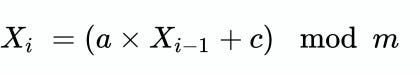
Where a, c and m are integers, and where X is the seed value of the series. For example a=21, seed=35, c=31, and m=100 will generate the random values of (where the value of m will define the range of numbers):

66 17 88 79 90 21 72 43 34 45 76 27 98 89 0 31 82 53 44 55 86
37 8 99 10 41 92 63 54 65 96 47 18 9 20 51 2 73 64 75 6 57 28
19 30 61 12 83 74 85 16 67 38 29 40 71 22 93 84 95 26 77 48 39
50 81 32 3 94 5 36 87 58 49 60 91 42 13 4 15 46 97 68 59 70 1
52 23 14 25 56 7 78 69 80 11 62 33 24 35

To prove this we can take the first three values:

(21x35+31) mod 100 gives 66
(21x66+31) mod 100 gives 17
(21x17+31) mod 100 gives 88
and so on.

If we make one change of a=22 we get:

1 53 97 65 61 73 37 45 21 93 77 25 81 13 17 5 41 33 57 85
1 53 97 65 61 73 37 45 21 93 77 25 81 13 17 5 41 33 57 85
1 53 97 65 61 73 37 45 21 93 77 25 81 13 17 5 41 33 57 85
1 53 97 65 61 73 37 45 21 93 77 25 81 13 17 5 41 33 57 85
1 53 97 65 61 73 37 45 21 93 77 25 81 13 17 5 41 33 57 85

This is an unacceptable value, as the sequence repeats. The basic rule is that c shares no common factors with m. Our real examples will have large and safe values, for example a=2,175,143, seed=3553, c=10,653, and m=1,000,000:

293732 114329 934700 172753 489332 85129 759100 61953 644932
335929 623500 671153 760532 866729 527900 353 836132 677529
472300 49553 871732 768329 456700 818753 867332 139129 481100
307953 822932 789929 545500 517153 738532 720729 649900 446353
614132 931529 794300 95553 449732 422329 978700 464753 245332
193129 203100 553953 932 243929 467500 363153 716532 574729
771900 892353 392132 185529 116300 141553 27732 76329 500700
110753 623332 247129 925100 799953 178932 697929 389500 209153
694532 428729 893900 338353 170132 439529 438300 187553 605732
730329 22700 756753 1332 301129 647100 45953 356932 151929 311500
55153 672532 282729 15900 784353 948132 693529 760300 233553

If you want to try your own example, try here.

The following is an outline of the code:

import sys
import math

values = [5,125,10,1,32, 101,33, 54,200,230,215,93,50,100,3,6,43]

max=255.0
inval=0
outval=0
ptr=0

print "Values:",values

print "Pairs:"
print "\tX\t\Y\tZ:"

for i in range(0,len(values)/2):
	x = (values[ptr]-max/2)/(max/2)
	y = (values[ptr+1]-max/2)/(max/2)

	z = math.sqrt(x*x+y*y)
	print "\t",round(x,3),"\t",round(y,3),"\t",round(z,3)
	if (z<1):
		inval=inval+1
	else:
		outval=outval+1
	ptr=ptr+2

print "\nInval:",inval," Outval:",outval

print "\nResult: ",4.0*inval/(inval+outval)

A sample run for values of 5, 125, 10, 1, 32, 101, 33, 54, 200, 230, 215, 93, 50, 100, 3, 6, 43 is:

First Five Pairs:
        X       Y       Z:
        -0.961  -0.02   0.961
        -0.922  -0.992  1.354
        -0.749  -0.208  0.777
        -0.741  -0.576  0.939
        0.569   0.804   0.985

Inval: 6  Outval: 2

Result:  3.0

Conclusions

In high-risk situations, software developers really need to understand how their random number generator is working, otherwise, it might be possible to win the lottery, just by analysing the code involved.

In cryptography, we often generate encryption keys from a random number or create a nonce (a random seed for a transaction), and these numbers are not quite random, it can compromise the whole process.