Towards a Fair and Open Election

A demo of the methods involved in this article is here.

Towards a Fair and Open Election

A demo of the methods involved in this article is here.

Our election processes are often archaic, where we still put a cross on a piece of paper and then wait for it to be manually counted. Then we must compile all the results from different voting stations and again wait for the result to be compiled. We must then hope that the whole infrastructure is fair and honest in the way that the votes are collected and counted.

But why shouldn’t each citizen have their vote to be completely anonymous and after the votes have been cast, for every citizen to view the result? The instance the votes are finalised, every citizen could then view the result, without waiting for a government to count and process the votes. It might be possible for us to, to “peek” at the votes currently cast, without actually knowing who had currently voted.

Let’s look at an example, where Bob, Alice and Eve want to vote but to keep their votes secret. Once all the votes have been cast, they should then be able to see the result, without actually revealing the voting intents (normally we would have a much larger population, of course, and the larger the population, the greater the anonymity will be):

In order to illustrate the voting process, I have created a simple example to illustrate using this [paper] and which was recently used by researchers at Newcastle University [paper] as part of The Economist Challenge on voting:

The maths involve a bit of understanding of discrete logarithms (please contact me if you want to learn a bit about his). Please also excuse the copy-and-paste graphics, as Medium doesn’t implement maths layout. The code that follows, though, is my own and is unique in illustrating a simple example.

Initially, we pick a safe value of g and a prime number p. I have selected g=2 and p=67 (if you want to see how to pick g, watch here). We then define a number of voters, who generate a random value (xᵢ). They then broadcast the value of:

It should not be possible to determine xi given Publici. Each voter keeps their xi value secret, and will prove to Trent that they know it (using Zero Knowledge Proof — ZPF).

Next all the votes regenerate a set of new keys:

This is the multiplication symbol, where we multiply the values of gxi

from 1 to i-1 and divide for i+1 to n. Within discrete logarithms, the divide operation is an inverse function. I appreciate that this bit of maths look a bit strange so here is the Python code that I created:

# Bill Buchanan Code

import random
import math
import sys

g=2
p=67

nvoters = 5
voter = [int] * nvoters
public = [int] * nvoters
Y = [int] * nvoters
make_votes = [int] * nvoters
vote = [int] * nvoters

vote[0]=0
vote[1]=0
vote[2]=0
vote[3]=0
vote[4]=0

def extended_euclidean_algorithm(a, b):
    """
    Returns a three-tuple (gcd, x, y) such that
    a * x + b * y == gcd, where gcd is the greatest
    common divisor of a and b.

    This function implements the extended Euclidean
    algorithm and runs in O(log b) in the worst case.
    """
    s, old_s = 0, 1
    t, old_t = 1, 0
    r, old_r = b, a

    while r != 0:
        quotient = old_r // r
        old_r, r = r, old_r - quotient * r
        old_s, s = s, old_s - quotient * s
        old_t, t = t, old_t - quotient * t

    return old_r, old_s, old_t

def inverse_of(n, p):
    """
    Returns the multiplicative inverse of
    n modulo p.

    This function returns an integer m such that
    (n * m) % p == 1.
    """
    gcd, x, y = extended_euclidean_algorithm(n, p)
    assert (n * x + p * y) % p == gcd

    if gcd != 1:
        # Either n is 0, or p is not a prime number.
        raise ValueError(
            '{} has no multiplicative inverse '
            'modulo {}'.format(n, p))
    else:
        return x % p

print "Votes: ",vote[0],vote[1],vote[2],vote[3],vote[4]

print "----"
for i in range(0,nvoters):
	voter[i] = random.randint(1, 30)

for i in range(0,nvoters):
	public[i] = g**voter[i]  % p

for i in range(0,nvoters):
	Y[i]=1

	for j in range(0,i): 
		Y[i] = (Y[i] * public[j]) % p
	for j in range(i+1,nvoters):
		Y[i] = Y[i] * inverse_of(public[j],p) % p

for i in range(0,nvoters):
	print "Public value: ",public[i]

for i in range(0,nvoters):
	print "Y value: ",Y[i]

for i in range(0,nvoters):
	make_votes[i] = (Y[i]**voter[i])*(g**vote[i]) % p

result = make_votes[0]

for i in range(1,nvoters):
	result = (result *make_votes[i]) % p

for i in range(0,nvoters):
	print "Vote ",make_votes[i]

print "---"
print "Vote tally: ",math.log(result)/math.log(g)

Once ready, the voters then create:

and where vᵢ is the vote for voter i. In discrete logs:

is the same as:

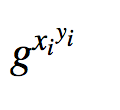
If you look at the code, this is coded as:

make_votes[i] = (Y[i]**voter[i])*(g**vote[i]) % p

Once all the votes are created we then compute the sum of the votes and which results in:

We then just take the inverse log, and we can determine the votes:

print "Vote tally: ",math.log(result)/math.log(g)

Here is a test run for all No votes:

Votes:  0 0 0 0 0
----
Public value:  36
Public value:  19
Public value:  23
Public value:  52
Public value:  64
Y value:  2
Y value:  28
Y value:  42
Y value:  49
Y value:  61
Vote  36
Vote  54
Vote  62
Vote  24
Vote  24
---
Vote tally:  0.0

and then for all “Yes”:

Votes:  1 1 1 1 1
----
Public value:  10
Public value:  8
Public value:  61
Public value:  43
Public value:  38
Y value:  59
Y value:  30
Y value:  34
Y value:  5
Y value:  63
Vote  57
Vote  65
Vote  22
Vote  16
Vote  60
---
Vote tally:  5.0

A demo of the methods involved in this article is here.

Presentation

References

Hao, Feng, Peter YA Ryan, and P. Zieliński. “Anonymous voting by two-round public discussion.” IET Information Security 4.2 (2010): 62–67. [paper]
McCorry, Patrick, Siamak F. Shahandashti, and Feng Hao. “A Smart Contract for Boardroom Voting with Maximum Voter Privacy.” IACR Cryptology ePrint Archive 2017 (2017): 110. [paper]