Visual One of the Most Beautiful Things in Cybersecurity

Visualising One of the Most Beautiful Things in Cybersecurity

We love things that are beautifully crafted and design. Unfortunately the world of cybersecurity is often tainted by cybercriminals, Tor networks hiding drug dealing, and cryptocurrency mining on our computers. But there is beauty to be found, and that beauty lies in the heart of elliptic curve cryptography (ECC). While some may want to spy on your every on-line action, it is ECC that is currently holding up our rights to privacy, and to properly identity our transactions and our identities.

Few things in this world holds up our rights than ECC.

You must thus thank ECC whenever you connect to your corporate wifi network, or to your VPN server in your local coffee shop. Behind them is ECC working hard in generating a new encryption key every time you connect to a Web site (ECDH), and leaving those who want to spy on us scratching their heads. And for our transactions, it is ECC again which makes sure that we properly identity senders and receivers. ECC cares little for a world build with false trust identities — such as with IBAN and CVV2 numbers — and signs for things with true digital trust.

And so we end up with these values that define an elliptic curve (p,a,b,gx,gy,n), and where a and b are the values used in:

y² = x³+ax +b (mod p)

All our operations are performed with (mod p), and where (gx,gy) is a base point on our curve.

If we plot our equation of y² = x³ +7, we get a nice curve of [here]:

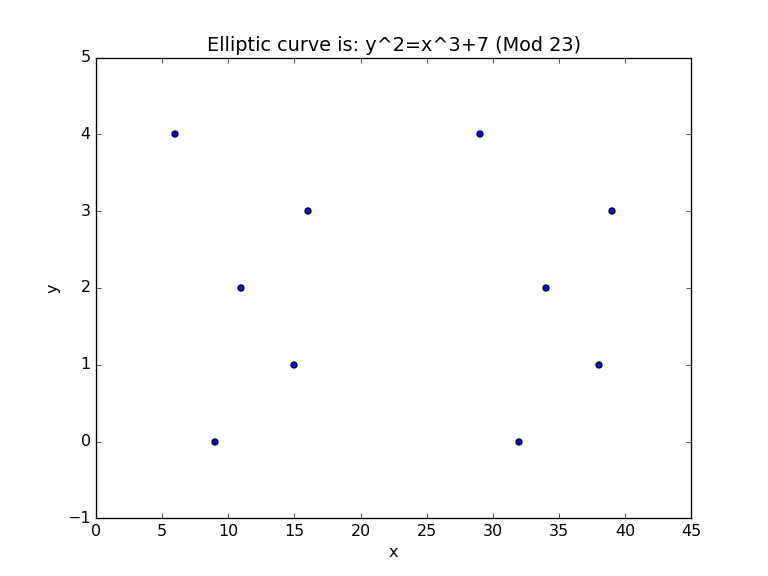
But, wait, we also have (mod p), and where we use a prime number. So let’s give these a go. First with a prime of 23 [here]:

The points we get are:

( 1 , 13 ) ( 4 , 18 ) ( 6 , 4 ) ( 8 , 6 ) ( 10 , 8 ) ( 11 , 2 ) ( 15 , 1 ) ( 16 , 3 ) ( 19 , 9 ) ( 20 , 16 ) ( 22 , 12 ) ( 24 , 13 ) ( 27 , 18 ) ( 29 , 4 ) ( 31 , 6 ) ( 33 , 8 ) ( 34 , 2 ) ( 38 , 1 ) ( 39 , 3 ) ( 42 , 9 ) ( 43 , 1

Now we can see that there is not an x-value for every y, as we need to find an integer which matches a square root of a mod value:

y² = val (mod p)

In the case of x=1, the result is 1³+7=8. If we take 13²(mod 23) we get 8.

So now let’s try a few more [here]:

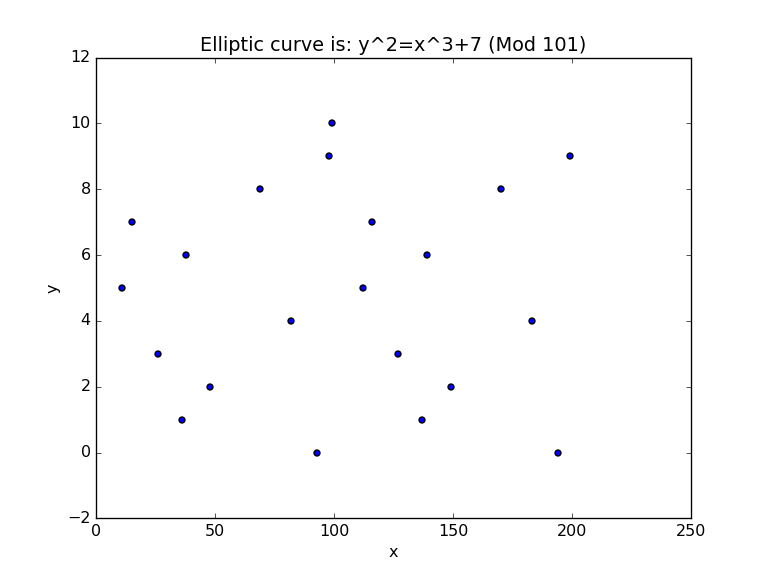
And [here]:

Elliptic curve cryptography is now at the forefront of privacy and security on the Internet. You will find it in Bitcoin, Blockchain, Tor, IoT device, and many other things. It is at the core of many new methods, so go learn it: