Learning With Errors (LWE) and Ring LWE

Learning With Errors (LWE) and Ring LWE
The method describing LWE is defined here.
Learning With Errors (LWE) is a quantum robust method of cryptography. It is also used within homomorphic encryption. Initially we create a secret key value (s) and another value (e). Next we select a number of values (A[]) and calculate B[] = A[] x s + e. The values of A[] and B[] become our public key. If s is a single value, A and B are one dimensional matrices. If we select s to be a one-dimensional matrix, A will be a two-dimensional matrix, and B will be a one-dimensional matrix.
Outline
Learning with errors is a method defined by Oded Regev in 2005 [here] and is known as LWE (Learning With Errors). It involves the difficulty of finding the values which solve:
B=A×s+e
where you know A and B. The value of s becomes the secret values (or the secret key), and A and B can become the public key.
Slides: [here]
Basics for LWE
To illustrate the method — and prove the results — I will use the examples defined here. The following code implements a basic LWE method:
import numpy as np
import sys
q=13
A=np.array([[4 ,1, 11, 10],[5, 5 ,9 ,5],[3, 9 ,0 ,10],[1, 3 ,3 ,2],[12, 7 ,3 ,4],[6, 5 ,11 ,4],[3, 3, 5, 0]])
sA = np.array([[6],[9],[11],[11]])
eA = np.array([[0],[-1],[1],[1],[1],[0],[-1]])
bA = np.matmul(A,sA)%q
print bA
bA = np.add(bA,eA)%q
print "Print output\n",bA
The output of this is:
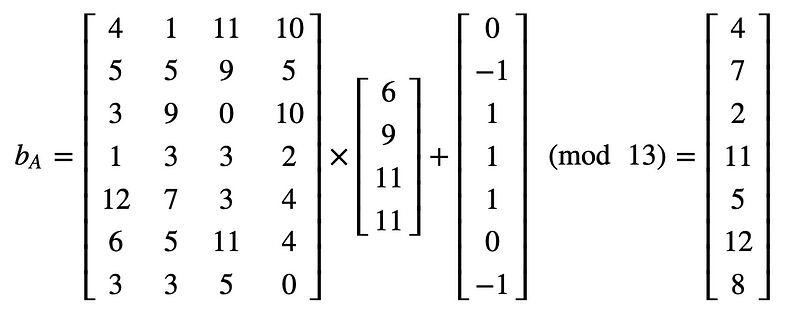
The following code implements a basic Ring LWE method:
A = [4,1,11,10]
sA = [6,9,11,11]
eA =[0,-1,1,1]
n=4
print A,sA,eA
xN_1 = [1] + [0] * (n-1) + [1]
print xN_1
A = np.floor(p.polydiv(A,xN_1)[1])
bA = p.polymul(A,sA)%q
bA = np.floor(p.polydiv(bA,xN_1)[1])
bA = p.polyadd(bA,eA)%q
bA = np.floor(p.polydiv(bA,xN_1)[1])
print "Print output\n",bA
In this method we perform a similar method to the Diffie Hellman method, but use Ring Learning With Errors (RLWE). With RLWE we use the coefficients of polynomials and which can be added and multiplied within a finite field (Fq) [theory] and where all the coefficients will be less than q. Initially Alice and Bob agree on a complexity value of n, and which is the highest co-efficient power to be used. They then generate q which is 2^n−1. All the polynomial operations will then be conducted with a modulus of q and where the largest coefficient value will be q−1. She then creates a_i(x) which is a set of polynomial values:

Next Alice will divide by Φ(x), which is x^n+1:

In Python this is achieved with:
xN_1 = [1] + [0] * (n-1) + [1]
A = np.floor(p.polydiv(A,xN_1)[1])
Alice now generates an error polynomial (e) and a secret polynomial (s):

Alice now creates b_A which is a polynomial created from A, e_A and s_A:

In coding this is defined as:
bA = p.polymul(A,sA)%q
bA = np.floor(p.polydiv(sA,xN_1)[1])
bA = p.polyadd(bA,eA)%q
Bob now generates his own error polynomial e′ and a secret polynomial s′:

Alice shares A with Bob, and Bob now creates b_B which is a polynomial created from A, e_B and s_B:

The code for this is:
sB = gen_poly(n,q)
eB = gen_poly(n,q)
bB = p.polymul(A,sB)%q
bB = np.floor(p.polydiv(sB,xN_1)[1])
bB = p.polyadd(bB,eB)%q
Alice then takes Bob’s value (b_B) and multiplies by s_A and divides by xn+1:

Bob then takes Alice’s value (b_A) and multiplies by s_B and divides by xn+1:
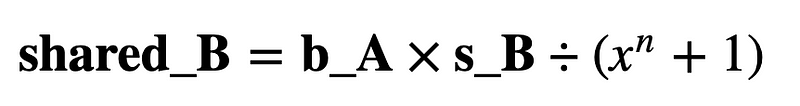
At the end of this, Bob and Alice will have the same shared value (and thus can create a shared key based on it).
In code this is:
sharedAlice = np.floor(p.polymul(sA,bB)%q)
sharedAlice = np.floor(p.polydiv(sharedAlice,xN_1)[1])%q
sharedBob = np.floor(p.polymul(sB,bA)%q)
sharedBob = np.floor(p.polydiv(sharedBob,xN_1)[1])%q
Conclusions
As our existing public cryptography methods are at risk, LWE looks to be a good solution in creating quantum robust cryptography.
The method describing LWE is defined here.