Ring Learning With Errors for Key Exchange (RLWE-KEX)

Ring Learning With Errors for Key Exchange (RLWE-KEX)
Public key and key exchange methods which use Diffie-Hellman, Elliptic Curve, RSA and El Gamal will be cracked by quantum computers. In order to overcome this we need new methods which are quantum robust. One of these methods is Learning With Errors (LWE). With RLWE we use the learning with errors (LWE) method but add polynomial rings over finite fields.
If you want to understand LWE, click [here].
Let’s say that Bob and Alice want to create a shared encryption key. In this case, Bob and Alice agree on shared values of A, n and q, and each of them generate error values (e) and secret values (s). They then calculate b based on A, and their own values of e and s. After this they exchange their values of b and calculate new values with the b values they have received and their own secret values. After this they will generate the same shared key.
In this method we perform a similar method to the Diffie Hellman method, but use Ring Learning With Errors (RLWE). With RLWE we use the coefficients of polynomials and which can be added and multiplied within a finite field (Fq) [theory] and where all the coefficients will be less than q. Initially Alice and Bob agree on a complexity value of n, and which is the highest co-efficient power to be used. They then generate q which is 2^n−1. All the polynomial operations will then be conducted with a modulus of q and where the largest coefficient value will be q−1. She then creates a_i(x) which is a set of polynomial values:

Next Alice will divide by Φ(x), which is xn+1:

In Python this is achieved with:
xN_1 = [1] + [0] * (n-1) + [1]
A = np.floor(p.polydiv(A,xN_1)[1])
Alice now generates an error polynomial (e) and a secret polynomial (s):

Alice now creates bA which is a polynomial created from A, textbf(eA and s_A :

In coding this is defined as:
bA = p.polymul(A,sA)%q
bA = np.floor(p.polydiv(sA,xN_1)[1])
bA = p.polyadd(bA,eA)%q
Bob now generates his own error polynomial e′ and a secret polynomial s′ :

Alice shares A with Bob, and Bob now creates b_B which is a polynomial created from A, e_B and s_B:
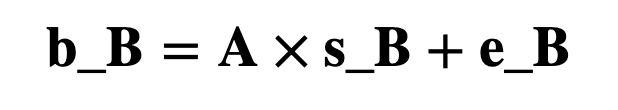
The code for this is:
sB = gen_poly(n,q)
eB = gen_poly(n,q)
bB = p.polymul(A,sB)%q
bB = np.floor(p.polydiv(sB,xN_1)[1])
bB = p.polyadd(bB,eB)%q
Alice then takes Bob’s value (b_B) and multiplies by s_A and divides by xn+1:

Bob then takes Alice’s value (b_A) and multiplies by s_B and divides by xn+1:

At the end of this, Bob and Alice will have the same shared value (and thus can create a shared key based on it).
In code this is:
sharedAlice = np.floor(p.polymul(sA,bB)%q)
sharedAlice = np.floor(p.polydiv(sharedAlice,xN_1)[1])%q
sharedBob = np.floor(p.polymul(sB,bA)%q)
sharedBob = np.floor(p.polydiv(sharedBob,xN_1)[1])%q
For 128 bits of equivalent security, we use n = 512, q = 25,601, and Φ(x)=x^512+1
For 256 bits of equivalent security, we use n = 512, q = 40,961, and Φ(x)=x^1024+1
A sample run with n=10, and q=210+1 shows that Alice and Bob have the same shared secret (1110110111):
q value: 1023 (2^ 10 +1)
n value: 10 (number of bits in polynomials)
A: 10 | [ 328. 426. 37. 911. 171. 913. 425. 569. 279. 344.]
-Alice---
s: 10 | [ 1. -1. -1. -2. -1. -1. -2. -2. 1. -1.]
e: 10 | [ 0. 1. 2. -1. -1. 0. 0. -2. 0. -1.]
b: 10 | [ 1.00000000e+00 0.00000000e+00 1.00000000e+00 1.02000000e+03
1.02100000e+03 1.02200000e+03 1.02100000e+03 1.01900000e+03
1.00000000e+00 1.02100000e+03]
-Bob---
s': 10 | [ 0. -1. 0. 0. 0. -3. 1. 0. -1. 0.]
e': 10 | [-1. -2. -1. 0. -2. -1. 0. -1. 0. -1.]
b': 10 | [ 1.02200000e+03 1.02000000e+03 1.02200000e+03 0.00000000e+00
1.02100000e+03 1.01900000e+03 1.00000000e+00 1.02200000e+03
1.02200000e+03 1.02200000e+03]
u : 10 | [1 1 1 0 1 1 0 1 1 1]
Shared Secret Alice: 10 | [ 1. 1. 1. 0. 1. 1. 0. 1. 1. 1.]
Shared Secret Bob: 10 | [ 1. 1. 1. 0. 1. 1. 0. 1. 1. 1.]
The following is an outline (based on code [here]):
import numpy as np
import sys
from numpy.polynomial import polynomial as p
n = 1024
qval = 32
q = 2**qval-1
xN_1 = [1] + [0] * (n-1) + [1] # (x^n + 1)
def gen_poly(n,q):
global xN_1
l = 0 #Gamma Distribution Location (Mean "center" of dist.)
poly = np.floor(np.random.normal(l,size=(n)))
while (len(poly) != n):
poly = np.floor(np.random.normal(l,size=(n)))
poly = np.floor(p.polydiv(poly,xN_1)[1]%q)
return poly
#Generate A
A = np.floor(np.random.random(size=(n))*q)%q
A = np.floor(p.polydiv(A,xN_1)[1])
#Alice (Secret & Error)
sA = gen_poly(n,q)
eA = gen_poly(n,q)
bA = p.polymul(A,sA)%q
bA = np.floor(p.polydiv(sA,xN_1)[1])
bA = p.polyadd(bA,eA)%q
#Bob
sB = gen_poly(n,q)
eB = gen_poly(n,q)
bB = p.polymul(A,sB)%q
bB = np.floor(p.polydiv(sB,xN_1)[1])
bB = p.polyadd(bB,eB)%q
#Shared Secret
#Alice
sharedAlice = np.floor(p.polymul(sA,bB)%q)
sharedAlice = np.floor(p.polydiv(sharedAlice,xN_1)[1])%q #TODO FIX THIS HAS TO BE DIVED BY HELPER
sharedBob = np.floor(p.polymul(sB,bA)%q)
sharedBob = np.floor(p.polydiv(sharedBob,xN_1)[1])%q
#Error Rounding
#--Bob
u = np.asarray([0] * n)
i = 0
while (i < len(u)):
if (len(bB) <= i): break;
if (int(bB[i]/(q/4)) == 0): u[i] = 0
elif (int(bB[i]/(q/2)) == 0): u[i] = 1
elif (int(bB[i]/(3*q/4)) == 0): u[i] = 0
elif (int(bB[i]/(q)) == 0): u[i] = 1
else:
print "error! (1)"
i+=1
i = 0
while (i < len(u)):
#Region 0 (0 --- q/4 and q/2 --- 3q/4)
if (u[i] == 0):
if (sharedBob[i] >= q*0.125 and sharedBob[i] < q*0.625):
sharedBob[i] = 1
else:
sharedBob[i] = 0
#Region 1 (q/4 --- q/2 and 3q/4 --- q)
elif (u[i] == 1):
if (sharedBob[i] >= q*0.875 and sharedBob[i] < q*0.375):
sharedBob[i] = 0
else:
sharedBob[i] = 1
else:
print "error! (2)"
i += 1
#--Alice
i = 0
while (i < len(u)):
#Region 0 (0 --- q/4 and q/2 --- 3q/4)
if (u[i] == 0):
if (sharedAlice[i] >= q*0.125 and sharedAlice[i] < q*0.625):
sharedAlice[i] = 1
else:
sharedAlice[i] = 0
#Region 1 (q/4 --- q/2 and 3q/4 --- q)
elif (u[i] == 1):
if (sharedAlice[i] >= q*0.875 and sharedAlice[i] < q*0.375):
sharedAlice[i] = 0
else:
sharedAlice[i] = 1
else:
print "error! (3)"
i += 1
#
print "A:",len(A),"|",A
print "\n-Alice---"
print " s:",len(sA),"|",sA
print " e:",len(eA),"|",eA
print " b:",len(bA),"|",bA
print "\n-Bob---"
print " s':",len(sB),"|",sB
print " e':",len(eB),"|",eB
print " b':",len(bB),"|",bB
print " u :",len(u),"|",u
print "\n"
print "Shared Secret Alice:",len(sharedAlice),"|",sharedAlice
print "Shared Secret Bob:",len(sharedBob),"|",sharedBob
print "\n\n--Verification--"
i = 0
while (i < len(sharedBob)):
if (sharedAlice[i] != sharedBob[i]):
print "Error at index",i
i+=1
Conclusions
The Diffie-Hellman method has done us well over the years, but it is on the risk list, and needs to be migrated away from. LWE provides one way of producing a quantum robust key exchange system.