When Mathematical Beauty Protects On-line Security and Identity: Point Addition In ECC

When Mathematical Beauty Protects Your On-line Security and Identity: Point Addition In ECC
Much of our on-line privacy is created by Elliptic Curve Cryptography. It is there when we need to negotiate in creating with secret key for HTTPs (with ECDH) and it is there when we want to sign for something (with ECDSA). At the core of what it does is the equation:
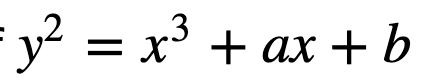
We then define a finite field bounded by a prime number p, so that our operations are done with (mod p). Within ECC, we typically have a base point (P), and then add this multiple time (n) to give nP. The value of nP is our public key, and the value of n is our private key.
For ECC, we calculate using x³+ax+b (mod p). For point addition of P (x,y) for the same point (2P). For this we have:
2P=(x_2,y_2)
Let s=(3x²+a)/(2y)
Then:
x_2=s_2−2x
y_2=s(x−x_2)−y
And that’s it. So let’s create some Python code to achieve this (I have highlighted the bits that relate to the equations above) [here]:
import sys
a=0
b=7
p=37
x=6
if (len(sys.argv)>1):
x=int(sys.argv[1])
if (len(sys.argv)>2):
p=int(sys.argv[2])
if (len(sys.argv)>3):
a=int(sys.argv[3])
if (len(sys.argv)>4):
b=int(sys.argv[4])
def modular_sqrt(a, p):
""" Find a quadratic residue (mod p) of 'a'. p
must be an odd prime.
Solve the congruence of the form:
x^2 = a (mod p)
And returns x. Note that p - x is also a root.
0 is returned is no square root exists for
these a and p.
The Tonelli-Shanks algorithm is used (except
for some simple cases in which the solution
is known from an identity). This algorithm
runs in polynomial time (unless the
generalized Riemann hypothesis is false).
"""
# Simple cases
#
if legendre_symbol(a, p) != 1:
return 0
elif a == 0:
return 0
elif p == 2:
return p
elif p % 4 == 3:
return pow(a, (p + 1) / 4, p)
# Partition p-1 to s * 2^e for an odd s (i.e.
# reduce all the powers of 2 from p-1)
#
s = p - 1
e = 0
while s % 2 == 0:
s /= 2
e += 1
# Find some 'n' with a legendre symbol n|p = -1.
# Shouldn't take long.
#
n = 2
while legendre_symbol(n, p) != -1:
n += 1
# Here be dragons!
# Read the paper "Square roots from 1; 24, 51,
# 10 to Dan Shanks" by Ezra Brown for more
# information
#
# x is a guess of the square root that gets better
# with each iteration.
# b is the "fudge factor" - by how much we're off
# with the guess. The invariant x^2 = ab (mod p)
# is maintained throughout the loop.
# g is used for successive powers of n to update
# both a and b
# r is the exponent - decreases with each update
#
x = pow(a, (s + 1) / 2, p)
b = pow(a, s, p)
g = pow(n, s, p)
r = e
while True:
t = b
m = 0
for m in xrange(r):
if t == 1:
break
t = pow(t, 2, p)
if m == 0:
return x
gs = pow(g, 2 ** (r - m - 1), p)
g = (gs * gs) % p
x = (x * gs) % p
b = (b * g) % p
r = m
def legendre_symbol(a, p):
""" Compute the Legendre symbol a|p using
Euler's criterion. p is a prime, a is
relatively prime to p (if p divides
a, then a|p = 0)
Returns 1 if a has a square root modulo
p, -1 otherwise.
"""
ls = pow(a, (p - 1) / 2, p)
return -1 if ls == p - 1 else ls
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
print "x-point is not on the curve. Please select another point."
sys.exit()
else:
return x % m
z=(x**3 + a*x +b) % p
y=modular_sqrt(z, p)
s=((3*x**2)+a) * modinv(2*y,p)
x2=(s**2-2*x) % p
y2=((s*(x-x2))-y) % p
print "a=",a
print "b=",b
print "p=",p
print "s=",s
print "\nP=(",x,",",y,")"
print "2P=(",x2,",",y2,")"
print "\n=== Just checking for (x2, y2)."
print "These have to be the same, to prove that 2P is on the elliptic curve:"
print "\nx^3+ax+b (mod p)=",(x2**3+a*x+b) % p
print "y^2 (mod p)=", (y2**2)% p
So let’s take an x-point of 17, and see what the point (P) is and what 2P is [here]:
a= 0
b= 7
p= 37
s= 29478
P=( 17 , 6 )
2P=( 13 , 24 )
=== Just checking for (x2, y2).
These have to be the same, to prove that 2P is on the elliptic curve:
x^3+ax+b (mod p)= 21
y^2 (mod p)= 21
In this case P is on the curve, and so 2P will also be on the curve. P is (17,6) in this case, and 2P is (13,24).
The curve we have used (with p=37) is not secure, as someone could easily find out all the mappings of P to 2P, and thus find out P. In real life we use a prime number that is between 128 bits and 512 bits long. Some typical curves are SECP256k1 (used in Bitcoin), Curve 25519 (used in ECDSA — and which gets its name from its prime number: 2²⁵⁵-19) and NIST P-256. To do it for real is easy, as we just need to populate the code with a, b and p [here]:
if (p==1):
type='SECP256k1'
p=0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a=0
b=7
if (p==2):
type='Curve25519_Montgomery'
po = pow(2,255)-19
a =486662
b=1
if (p==3):
type='NIST P256'
a = -3
b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
if (p==4):
type='SECP160k1'
a = 0
b = 7
p = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFAC73
And a sample run:
Type: SECP256k1
a= 0
b= 7
p= 115792089237316195423570985008687907853269984665640564039457584007908834671663
x-point= 1
s= 309559869782811709114791466953038768572873897589664974937917787940921749681528
P=( 1 , 29896722852569046015560700294576055776214335159245303116488692907525646231534 )
2P=( 90462569716653277674664832038037428010367175520031690655826237506178777087235 , 30122570767565969031174451675354718271714177419582540229636601003470726681395 )
=== Just checking for (x2, y2).
These have to be the same, to prove that 2P is on the elliptic curve:
x^3+ax+b (mod p)= 64938697018864737649504516342305227130723343145766499186801514322306538536414
y^2 (mod p)= 64938697018864737649504516342305227130723343145766499186801514322306538536414
Conclusions
There are few things more beautiful in the operation and which protect your privacy and identity than Elliptic Curve Cryptography. John Napier would love seeing how our on-line world has evolved.