Adding Points in Elliptic Curve Cryptography

Adding Points in Elliptic Curve Cryptography

Much of our on-line privacy is now created by Elliptic Curve Cryptography (ECC). The world is fast moving towards public key encryption in order to create a more trusted world. It is there when we need to negotiate in creating a secret key for HTTPs (with ECDH) and it is there when we want to sign for something (with ECDSA). It provides the core security of blockchain, and is in virtually every bit of trust within cryptocurrency transactions.

The world is generally moving away from RSA, is it has not scaled into a modern world, and is now often too cumbersome to be used in many applications. New applications, too, have been generated from the core properties of ECC. The Pedersen Commitment, for example, allows us to blind data but still make commitments, and the Schnorr signing method allows us to take many public keys and merge them into a single signature.

At the core of what it does is the equation:

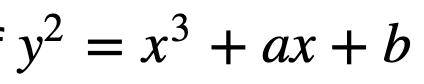
We then define a finite field bounded by a prime number p, so that our operations are done with (mod p). Within ECC, we typically have a base point (P), and then add this multiple time (n) to give nP. The value of nP is our public key, and the value of n is our private key.

For point addition, we take two points on the elliptic curve and then add them together (R=P+Q).

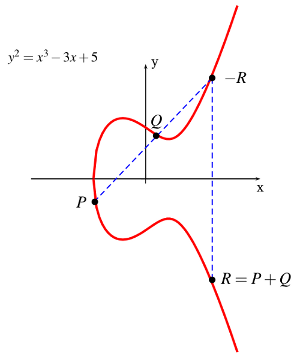
So if we use x³+ax+b (mod p), and we have two points P (x1,y1) and Q(x2,y2) that we want to add, we calculate the gradient between the points:

s=(y1−y2)/(x1−x2)

Then to determine the new point R(x3,y3), we use:

x3=s²−x1−x2

y3=s(x1−x2)−y1

And that’s it. So let’s create some Python code to achieve this (I have highlighted the bits that relate to the equations above) [here]:

import sys

a=0
b=7
p=37

x1=6
x2=8

if (len(sys.argv)>1):
    x1=int(sys.argv[1])
if (len(sys.argv)>2):
    x2=int(sys.argv[2])
if (len(sys.argv)>3):
    p=int(sys.argv[3])
if (len(sys.argv)>4):
    a=int(sys.argv[4])
if (len(sys.argv)>5):
    b=int(sys.argv[5])
    

def modular_sqrt(a, p):
    """ Find a quadratic residue (mod p) of 'a'. p
        must be an odd prime.

        Solve the congruence of the form:
            x^2 = a (mod p)
        And returns x. Note that p - x is also a root.

        0 is returned is no square root exists for
        these a and p.

        The Tonelli-Shanks algorithm is used (except
        for some simple cases in which the solution
        is known from an identity). This algorithm
        runs in polynomial time (unless the
        generalized Riemann hypothesis is false).
    """
    # Simple cases
    #
    if legendre_symbol(a, p) != 1:
        return 0
    elif a == 0:
        return 0
    elif p == 2:
        return p
    elif p % 4 == 3:
        return pow(a, (p + 1) / 4, p)

    # Partition p-1 to s * 2^e for an odd s (i.e.
    # reduce all the powers of 2 from p-1)
    #
    s = p - 1
    e = 0
    while s % 2 == 0:
        s /= 2
        e += 1

    # Find some 'n' with a legendre symbol n|p = -1.
    # Shouldn't take long.
    #
    n = 2
    while legendre_symbol(n, p) != -1:
        n += 1

    # Here be dragons!
    # Read the paper "Square roots from 1; 24, 51,
    # 10 to Dan Shanks" by Ezra Brown for more
    # information
    #

    # x is a guess of the square root that gets better
    # with each iteration.
    # b is the "fudge factor" - by how much we're off
    # with the guess. The invariant x^2 = ab (mod p)
    # is maintained throughout the loop.
    # g is used for successive powers of n to update
    # both a and b
    # r is the exponent - decreases with each update
    #
    x = pow(a, (s + 1) / 2, p)
    b = pow(a, s, p)
    g = pow(n, s, p)
    r = e

    while True:
        t = b
        m = 0
        for m in xrange(r):
            if t == 1:
                break
            t = pow(t, 2, p)

        if m == 0:
            return x

        gs = pow(g, 2 ** (r - m - 1), p)
        g = (gs * gs) % p
        x = (x * gs) % p
        b = (b * g) % p
        r = m


def legendre_symbol(a, p):
    """ Compute the Legendre symbol a|p using
        Euler's criterion. p is a prime, a is
        relatively prime to p (if p divides
        a, then a|p = 0)

        Returns 1 if a has a square root modulo
        p, -1 otherwise.
    """
    ls = pow(a, (p - 1) / 2, p)
    return -1 if ls == p - 1 else ls

def egcd(a, b):
    if a == 0:
        return (b, 0, 1)
    else:
        g, y, x = egcd(b % a, a)
        return (g, x - (b // a) * y, y)

def modinv(a, m):
    g, x, y = egcd(a, m)
    if g != 1:
        print "x-point is not on the curve. Please select another point."
    sys.exit()
    else: 
       return x % m

print "a=",a
print "b=",b
print "p=",p

print "x-point=",x1
print "x-point=",x2


z=(x1**3 + a*x1 +b) % p
y1=modular_sqrt(z, p)

z=(x2**3 + a*x2 +b) % p
y2=modular_sqrt(z, p)

print "\nP1\t(%d,%d)" % (x1,y1)
print "P2\t(%d,%d)" % (x2,y2)


    
s=(y2-y1)* modinv(x2-x1,p) 

x3=(s**2-x2-x1) % p

y3=((s*(x2-x3)-y2)) % p

print "P1+P2\t(%d,%d)" % (x3,y3)

And now, let’s say we have two points (6,1) and (8,1) on an elliptic curve of x³+7 (mod 37), the result is then (23,36) [here]:

a= 0
b= 7
p= 37
x-point= 6
x-point= 8

P1  (6,1)
P2  (8,1)
P1+P2   (23,36)

If you want to test this, try [here]. The great thing about point addition is that it is not possible to mathematically determine the two points which made the resultant point.

Conclusions

Some time, soon, we need to mark our existing data world as legacy, and need to migrate away from the simplistic way we capture, store and process data. It is a data model of the 1980s, and relates to a much simpler data world. In the 21st Century we now need to build new digital-focused societies, and public key encryption will be a core part of this. Leading the way is the wonderful ECC.

Go learn!