The Magic Of Bulletproofs

The Magic Of Bulletproofs
Towards True Cybersecurity
We live in a 1980s viewpoint of data.
Very little of our data transactions and logs can be truly trusted. Along with this, we also reveal a great deal of information in the records that we keep.
We thus need to move to a more trusted world, and where we can trust each transaction, but make sure they are privacy-preserving. We now see cryptocurrencies rushing to protect the details of transactions — such as with Ethereum using zkSnarks, Monero implementing Ring Signatures and Bulletproofs, and Bitcoin looking towards Mimblewimble. Our ledger will thus increasingly look like an anomyised list of transactions, and where the sender, the receiver and the transaction detail will be anonymised. At the core of much of this work is the CT (Confidential Transaction) and where we use Pedersen Commitments to blind the data.
Overall our data world of the future could look like this, and where we have an anonymised lowest layer, and then reveals parts of it to implement things like finance and health care:
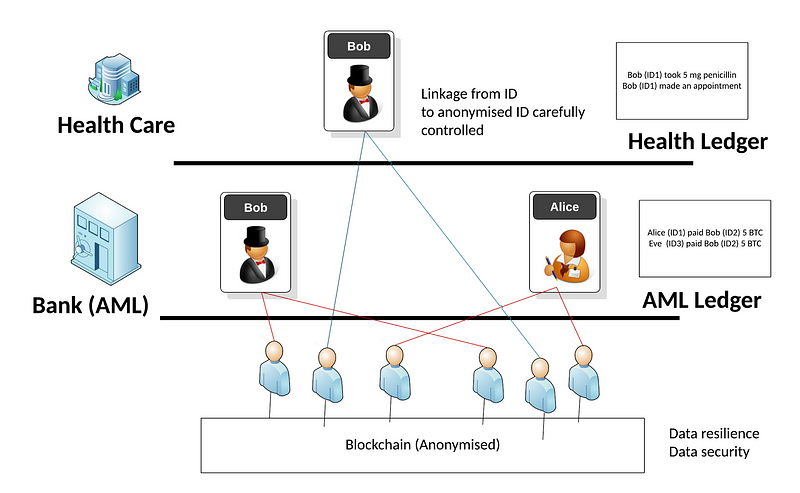
Only with the special secrets — the blinding factors — will we reveal the details. But we need to make sure that the transactions are still valid before they are enacted. For this we look to Bulletproofs as an efficient way of making sure that blinded transactions are still valid
Eve does Pedersen
Right. Eve The Magician asks the audience for a value of G, and Carol shouts out “5”. Eve then asks Alice to think of a number (a) and multiply the two values together to give y:
y = aG
“Don’t tell me the result”, says Eve. She now asks for another number from the audience, and they shout out “7”. Eve writes something on a piece of paper, and shouts out that her answer is “38”. She turns to Alice and asks her for the result of her calculation, and she says that y is “10”. The audience are worried that Eve has failed in her trick.
“But”, she says, “my card says a value of ‘4’”, and she shows this to the audience, “Now please calculate z, and which is aG + bH”. What is the value that you get?”. Alice calculates and shows her calculation:
“38”
“And that is the answer that I showed you before I knew Alice’s value”, says Eve to great applause. This the Pedersen Commitment in action, and where Eve committed to a value, and then blinding her guess. She then revealed her blinding factor, and showed that she knew the answer all along.
In this case Alice’s secret was “2” and Eve’s blinding factor was “4”, so Eve got:
z = aG + bH = 2*5 + 4 * 7 = 38
Eve knew that Alice was going to pick “2” (don’t ask why, as she is a magician), so she blinded it with “4”, and was able to show that she knew Alice’s value.
This is known as Pedersen Commitment — or nothing up my sleeve (NUMS) — and where we produce our commitment and then show the message that matches the commitment. In its core form, we can implement a Pedersen Commitment in discrete logs [here]. But blockchain, IoT, Tor, and many other application areas, now use elliptic curve methods, so let’s see if we can make a commitment with them.
Adding a blinding value
For this, we can obscure the values in a transaction by adding a blinding value. Let’s say that we have a transaction value of v, we can now define this as a point on the elliptic curve (H) as:
v×H
If we have three transactions (v1, v2 and v3), we can create a sum total of:
Total=v1×H+v2×H+v3×H=(v1+v2+v3)×H
We can thus determine the sum of the transactions. But we could eventually find-out the values of v1, v2 and v3, as they would always appear as the same value when multiplied by H. We can now add a blinding factor by adding a second point on another elliptic curve (G) and a private key (r). A transaction value is then (as defined as a Pedersen Commitment):
C = v×H+r×G
Let’s say that Bob has two input values (v1 and v2) and one output value (v3), and where v3= v1+v2. We can then create a blinding factor for each transaction:
C = (ri1×G+vi1×H)+(ri2×G+vi2×H)=(ro3×G+vo3×H)
Then:
ri1+ri2=ro3
In this case if we can prove this, we have proven that the inputs are equal to the outputs.
Bulletproofs and rangeproofs
Now, Pedersen Commitment size just keeps increasing for the number of transactions we are blinding. This was keenly felt by Monero, and where a consider amount of effort and space were taken up with the commitments. And so bulletproofs have been created to considerably reduce the size of the proof of the transaction.
Bulletproofs were created in 2017 by Stanford’s Applied Cryptography Group (ACG) [paper]. They define a zero-knowledge proof and where a value can be checked to see it it lies within a given range. The name of “bulletproofs” is defined as they are short like a bullet, and with bulletproof security assumptions. In the following we define the size of the bit vector and then check to see if a value is in that range — a range proof. If the bit vector is 8 bits long, then we will prove that the value lies between 0 and 255. A value larger than this will fail. The test is thus whether x∈[0,2^n−1], and where n is the number of bits in the bit vector.
I have created a demonstrator it in JavaScript here.
And a demonstrate in Go here.
The theory is beyond the scope of this article, but basically we perform a range proof on the input values and then create challenges which are then proven with IPP (inner produce proofs) [details]:
Value is : 128
Value is between 1 and 2^64-1: true
=== Public parameters:
Curve type: secp256k1
G: {73298500421277376770959725776538948598140332406732930337526636630574379309589 65361040670752309884639562177289034463290743352662500631474087478899695501860}
H: {84213878005907352693940005284807919553015103954531775028806101001657921307492 4853819773361621041359354585547033012654231597651644911911422070634871780388}
Curve b value: 7
Curve prime value: 115792089237316195423570985008687907853269984665640564039457584007908834671663
Gi[0]: {72242507303365076728861865557797731214902786606643414733580150814770869272593 27033601650718423694844620558628339447280369833685083662535239836251867410934}
Hi[0]: {5585562941503279596474839515994484383064083005553472397059910728304658620745 77310285201950507048734835505325678526225389174038208505235173650760230890492}
Vector length: 64
=== Proof
Challenge:
Cx: 58272614926395319959004507362753026724905829340363601981324802106298897908430
Cy: 49909396289108762784112513859562527170976130304793501415000016424255780151487
Cz: 107736957691413878072189052694497520008408003124327103973201024901484630638505
A: {45505696241792036671595145036491704484400729156330665018681572972515204440741 36835635329317526758225818054331438008312352037415813343602755142122425175641}
S: {7067584994623916005039987457298533639349317199159085210146080620052775759314 111586284366499266040095829291423462684751503917161755447718750035638709712846}
T1: {15860938041633320250734412146664591843196448598244389701671724923483013890235 85909311114202721738923368029826258629816798484385017756160430142359220386042}
T2: {11218978778992429881252403489569329985291630456368831946827522773162522791836 92986601520847539934299082411632916409669209681848891641612735379418812240346}
Tau: 31288499956408627728154390991400142510054834246241453786834058155151223711192
Th: 37874398250466195264831619433062977968002660212655492774387833033948151765944
Mu: 3671392883877886491895450062951187493857366687944882228826247466825963918461
IPP (Inner product proof):
a: 54937394546865235134629391637726158476031128595918527975889804497928878514532
b: 26017385586345100748521060073491138767409142292313773679708851452567041679986
L[0]: {76920586076624124411843424303015396631739105408092698367196982682970737207106 12390395095295003979006488468365009308528883680863800140977760775095980776438}
R[0]: {20455960824304832117456139493127263185860501108324533253528812536370213209363 70627273714857503369574274511587205010835658810501950837400963523068539003036}
L[1]: {23188263290132515159563188970321381916019468528653261910231289835152361611739 54211549768224747067733694108008660363938337301586439305527154701267039752124}
R[1]: {31581310422916786848753211208900862102617701544761557623777708030146610872290 87932225455053279071774798578000095066550779578219800985004699759191305369219}
The public parameters are [1]:
- l: cardinality of the subgroup of the elliptic curve used (Ed25519)
- N: bitsize of the elements whose range one wants to prove (N = 64)
- M: number of proofs to aggregate
- G: the base point of the subgroup of the elliptic curve used
- H: another generator of the subgroup of the elliptic curve used whose discrete log wrt G is not known and hard to find
- Gi: a list of M*N generators of the subgroup of the elliptic curve used whose discrete log wrt any other generator is not known and hard to find
- Hi: a list of M*N generators of the subgroup of the elliptic
The committed to values are [1]:
- v: the values to hide (and are in the range 0≤vj≤2N
- gamma: hiding values
The bulletproof is then [1]:
- V: a vector of curve points, Pedersen commitments to v[i] with hiding values gamma[i]
- A: a curve point, vector commitment to aL and aR with hiding value alpha
- S: a curve point, vector commitment to sL and sR with hiding value rho
- T1: a curve point, Pedersen commitment to t1 with hiding value tau1
- T2: a curve point, Pedersen commitment to t2 with hiding value tau2
- taux: a scalar, hiding value related to T1, T2, V and t
- mu: a scalar, hiding value related to A and S
- L: a vector of curve points of size log2(M*N) computed in the inner product protocol
- R: a vector of curve points of size log2(M*N) computed in the inner product protocol
- a: a scalar computed in the inner product protocol
- b: a scalar computed in the inner product protocol
- t: a scalar, inner product value to be verified
Basically we perform a folding process for the values within the commitment, and significantly reduce the space required.
Conclusions
We need to move to a more trusted world, and agree that the old data model of our world is finished. Our new model will integrate trust into our transactions, and break away from our centralised viewpoint of the world.
References
[1] Evaluation of Bulletproof Implementation, [here].