A Fairground Problem … BiBa

A Fairground Problem … BiBa
You are at a fairground, and there’s a fun challenge. In front of you are five bins, and the challenge is for you to fire a ball at the bins, and where they will fall randomly into one of the bins. If you get two balls in the bin, you will win, but every attempt will cost you $1. The prize money is $4. Is it a good bet?
Okay. You have five bins, and you want to get to the point where one bin has two balls. For this you will have a 1-in-5 probability that any throw of the ball will go into a specific bin. What is the likely number of throws that it will take to win? Well, as a maximum will be six throws (you will lose $6, but gain $4, and will be thus $2 down). As a minimum it will take you two throws (for a $2 stake you will win $4). Will you win or will the fairground win, overall?
Of course, the probability of you not winning on the first throw will be:
P_0 = 1
On the second we now have a 1-in-5 chance of getting in the bin we hit the first time, so the chances of us not winning will be:
P_1 (Not win on second throw) = 4/5
Now, on the third throw, if we have not won, we will have two bins with balls out of 5 bins. So the bins could be:
1 1 0 0 0
1 0 1 0 0
1 0 0 1 0
1 0 0 0 1
0 1 1 0 0
0 1 0 1 0
0 1 0 0 1
0 1 0 1 0
0 1 0 0 1
You have three spaces that we could hit in each of the bins. You thus have two chances to hit a bin with a ball, and three chances to miss. The chance of you not winning is 3/5. The probability you will not win at this point is thus:
P(Not win on third throw) = 4/5 x 3/5 = 12/25 = 0.48
The probably of you winning is 0.52, but it has cost you $3 to get to this point. A win is $4, so your returns — on average — will be $2.08 (you are likely to lose around half of your money at this stage, if you keep playing the game continually). If you are still in the game, you now have a 2-in-5 chance of losing. For example the losing bins will include:
1 1 1 0 0
1 1 0 1 0
1 0 1 1 0
0 1 1 1 0
1 1 0 1 0
Thus:
P(No win on forth throw) = 4/5 x 3/5 x 2/5 = 12/25 = 0.192
You now have a 80.8% chance to have won at this point. So for a $4 stake, your returns are still only likely to be $3.20 (on average you will be down by $0.8). Finally you throw again, and now only have a 1 in 5 chance of not hitting on a bin with a ball:
P(No win in five throws) = 4/5 x 3/5 x 2/5 x 1/5 = 12/25 = 0.0384
You now have a 96.1% chance to have won at this point. So for a $5 stake, your returns — on average — are still only likely to be $3.84 (you will be over $1 down for each attempt). And finally you throw the last one, and you are guaranteed to win — so you might as well pay your money — as you have been unlucky enough to throw the balls in all the bins:
P(No in five throws) = 4/5 x 3/5 x 2/5 x 1/5 x 0/5=0
You will then win, but it has cost you $6 and the return is $4. So it is a bad bet!
The coding to determine the average number of throws to get two balls in at least one bin, and with n bins is [here]:
n = 5.0
val=(n-1)/(n)
for i in range(2,int(n+2)):
print i,1-val
val = val* (n-i)/n
E=0
p_prev=1.0/n
E=p_prev*2
for i in range(2,int(n)):
pnew = p_prev*(n+1-i)*i/(n*(i-1))
E = E+pnew*(i+1)
p_prev=pnew
print "Average number of throws",E
A sample run for five bins is [here]:
Number of bins: 5
Throw Prob of winning
2 0.20
3 0.52
4 0.81
5 0.96
6 1.00
Average number of throws 3.28
This type of problem can be used to analyse hashing algorithms, and is the basis of the birthday paradox. With this, we determine the probability of two people having the same birthday. We then have 365 days, and so will have 365 bins:
Throw Prob of winning
2 0.003
3 0.008
4 0.016
5 0.027
6 0.040
7 0.056
8 0.074
9 0.095
10 0.117
11 0.141
12 0.167
13 0.194
14 0.223
15 0.253
16 0.284
17 0.315
18 0.347
19 0.379
20 0.411
21 0.444
22 0.476
23 0.507
24 0.538
25 0.569
We see that for 365 days, then for 23 people in a room, we have a 50.7% chance of a ‘collision’.
Another area is within the creation of a one-time signature (OTS) and is named “BiBa” (“Bins and Balls”) [here].
Basically we create a number of random values for our private key:
Priv = x_1, x_2, … x_n
Next we create our public key as hashed versions of our private key:
Pub = SHA1(x_1), SHA1(x_2) … SHA1(x_n)
To create the signature, we find two values which will create a collision:
H(M || x_i) == H(M || x_j)
We then publish (x_i, x_j)
It would be too difficult for Eve to find the values of x_i and x_j to create a collision.
Hash to Obtain Random Subset (HORS)
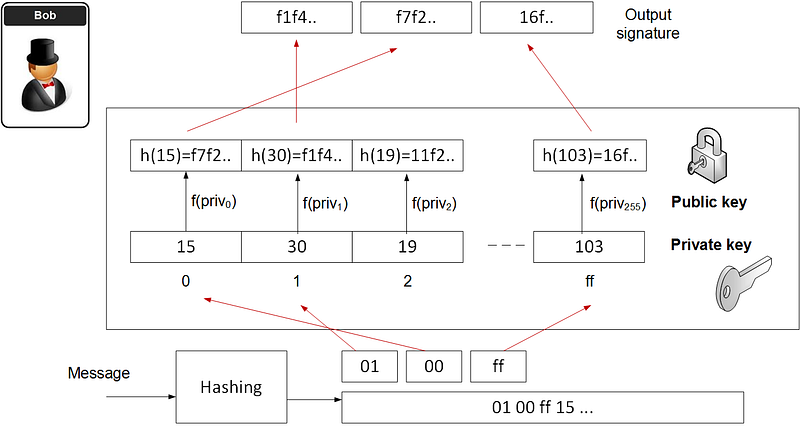
Hash to Obtain Random Subset (HORS) is one such quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
If we assume that we are going to segment the hash into 8-bit values and for a 128-bit hash (using MD5), the method is then:
- Create 256 random values. These are our private key values (priv0…priv255).
- Hash each of the private key values to produce a list of our public key values pub. These will be indexed.
- Hash the message (M) for a 128-bit hash (h), and which will produce 16 8-bit values (hi).
- Take each of the values (hi) and use as a look-up to the public key value.
If Bob creates the public key and the private key, then he creates the message, and then adds the hash-based signatures. He then shows Alice the message and the message, and his public key. Bob then shows that he has the associated private key for this public. He cannot use this key pair again, so will produce a new key pair for the next signature.
The following illustrates a simple example:
A sample run with “hello” is:
Byte values: 146 197 23 16 145 157 113 185 118 42 75 188 42 64 65 93
Private key: [36, 140, 153, 156, 175, 202, 73, 171, 214, 161, 0, 56, 19, 26, 121, 135, 207, 109, 89, 97, 152, 171, 207, 131, 122, 89, 256, 199, 49, 146, 234, 60, 243, 182, 45, 179, 166, 228, 44, 144, 140, 154, 2, 98, 5, 133, 139, 43, 73, 156, 143, 72, 189, 98, 219, 172, 169, 205, 47, 86, 86, 172, 114, 147, 58, 189, 224, 122, 54, 70, 196, 82, 239, 221, 87, 127, 77, 200, 115, 193, 103, 171, 52, 256, 149, 55, 85, 150, 248, 132, 202, 200, 56, 236, 95, 1, 31, 139, 255, 253, 233, 90, 113, 24, 232, 98, 160, 95, 185, 130, 211, 185, 147, 83, 5, 66, 56, 205, 12, 199, 148, 148, 204, 135, 214, 123, 122, 196, 209, 94, 42, 121, 123, 26, 17, 2, 61, 23, 172, 70, 76, 225, 164, 176, 159, 146, 231, 138, 18, 175, 238, 34, 33, 210, 213, 93, 36, 91, 250, 91, 202, 105, 254, 140, 209, 65, 48, 141, 198, 232, 211, 148, 38, 11, 178, 254, 212, 229, 30, 145, 19, 234, 250, 95, 164, 105, 161, 207, 141, 46, 72, 47, 31, 5, 187, 159, 68, 123, 91, 195, 125, 197, 189, 65, 176, 35, 84, 114, 138, 141, 116, 51, 155, 157, 195, 237, 211, 51, 99, 68, 220, 76, 34, 126, 189, 251, 189, 17, 256, 49, 131, 72, 62, 237, 59, 105, 211, 133, 223, 239, 198, 110, 193, 37, 178, 227, 65, 158, 29, 194, 87, 89, 206, 173, 253, 232]
Public key:
['19c', '138', 'b3e', '1c9', '821', '854', 'd2d', 'a4a', 'ca4', 'bd4', 'cfc', '9f6', '1f0', '4e7', '4c5', '7f1', '69a', '272', '764', 'e2e', '37a', 'a4a', '69a', '1af', 'a0a', '764', 'f71', '84d', 'f45', 'a5e', '289', '072', 'cb7', '4c5', '6c8', '8f5', '7e7', '74d', 'f71', '0a0', '138', '1d7', 'c81', 'ed3', 'e4d', '9fc', 'e00', '17e', 'd2d', '1c9', '903', '32b', 'a25', 'ed3', 'c0e', '1ff', '363', 'eae', '67c', '93d', '93d', '1ff', '5fd', '8d5', '66f', 'a25', '13f', 'a0a', 'a68', '7cb', '084', '977', '555', '060', 'c7e', 'ec5', '28d', '364', '2b4', 'bd6', '697', 'a4a', '9a1', 'f71', 'f22', 'b53', '3ef', '7ef', '621', '65d', '854', '364', '9f6', '011', '812', 'c4c', 'c16', 'e00', 'fe1', 'c24', 'e16', '861', '732', '1ff', 'be8', 'ed3', 'b73', '812', 'eec', '9b8', 'eb1', 'eec', '8d5', 'fe9', 'e4d', '329', '9f6', 'eae', 'c20', '84d', '47d', '47d', '274', '7f1', 'ca4', '202', 'a0a', '084', 'b1d', 'f4b', 'a1d', '4c5', '202', '4e7', '70e', 'c81', '7f3', '376', '1ff', '7cb', 'fbd', 'd1c', 'fa7', '38a', '140', 'a5e', '9b0', '013', '6f4', '821', 'ac1', 'e36', '182', '6f3', '979', '98d', '19c', '542', '6c9', '542', '854', '65b', 'c52', '138', 'b1d', 'fc4', '642', '0f2', '0e6', 'be8', 'eb1', '47d', 'a57', '651', '8f8', 'c52', '153', '57a', '341', '2b2', '1f0', '289', '6c9', '812', 'fa7', '65b', 'bd4', '69a', '0f2', 'd9d', '32b', '67c', 'c16', 'e4d', '31f', '140', 'a3f', '202', '542', '033', '3de', '85d', 'a25', 'fc4', '38a', '1c3', '68d', '5fd', '013', '0f2', 'c45', '283', '2a7', '6c4', '033', '539', 'eb1', '283', 'ac6', 'a3f', 'ec8', 'fbd', 'e36', '069', 'a25', '19f', 'a25', '70e', 'f71', 'f45', '1af', '32b', '44f', '539', '093', '65b', 'eb1', '9fc', '115', '555', '0e6', '5f9', 'bd6', 'a5b', '8f8', '705', 'fc4', '064', '6ea', 'a59', 'c7e', '764', '7ea', 'f7e', 'c24', 'be8']
Signature: ['32b', '7f1', '4c5', '5fd', '9b0', '364', 'f71', 'ed3', '1f0', 'b3e', '084', 'd1c', 'b3e', '67c', 'd9d', 'eb1']
A demonstration of this method is defined here.
Signing
HORS is a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key — the verification key. We then just use the private key of the OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path which leads to the root of the tree. At the receiver end, they can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
In a post quantum world, we need to find new ways of signing, which do not have a trap door, and BiBa related methods are an excellent choice.