How Do I Reveal How I Voted, But Still Keep My Vote Secret?

How Do I Reveal How I Voted, But Still Keep My Vote Secret?
A demo of the method I will show is here.
Well, the UK is going to the polls — again — on Thursday. So how can I reveal to you the way I voted, after the election, and by revealing my commitment within the voting process? For this, we could perform a one way hash of my vote, and then send you that:
commitment = Hash(“Labour”) or Hash(“Conservative”)
But you would be able to crack this, so I can add salt to the hash:
commitment = Hash(“Labour”+salt) | Hash(“Conservative”+salt)
I can then give you my commitment, and after the vote I can give you the salt value that I used, and you can check it. But let’s say that you do not trust the hashing process, or that I don’t want to reveal my statement for the vote. For this, we can use the Pedersen Commitment, and where I can commit a value, and then reveal my voting options at some time later.
In the Pedersen Commitment we take two large prime numbers (p and q) and and we create a generator value (g) which is of the order of q and a subgroup of Z∗p. Then s becomes a secret from 0 to Zq, and we calculate h=g^s(mod p). The values of (p,q,g,h) are public values.
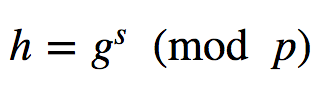
The sender now creates a commitment for a message (m) and with a random number (r):

The sender can then send c to the receiver. Next, the sender will then reveal m and r for the commitment, and the receiver verifies with:

If the values match, the sender has proven the commitment to the receiver. With the Pedersen Commitment we hide the message that is to be revealed, and where the recipient will not know the message until we reveal it.
Homomorphic properties
With the Pedersen Commitment we can also use as homomorphic encryption, and where we can add commitments, and which is equivalent to adding the values. In this way we could tally of the votes from the commitments of the voters, and then reveal the total.
The following provides some code [code][demo]:
from Crypto import Random
from Crypto.Random import random
from Crypto.Util import number
import sysdef generate(param):
q = param[1]
g = param[2]
h = param[3]
return q,g,hclass verifier:
def setup(self, security):
p = number.getPrime(2 * security, Random.new().read)
q = 2*p + 1
g = number.getRandomRange(1, q-1)
s = number.getRandomRange(1, q-1)
h = pow(g,s,q)
param = (p,q,g,h)
return param def open(self, param, c, x, *r):
result = "False"
q,g,h = generate(param) sum = 0
for i in r:
sum += i res = (pow(g,x,q) * pow(h,sum,q)) % q if(c == res):
result = "True"
return result def add(self, param, *cm):
addCM = 1
for x in cm:
addCM *= x
addCM = addCM % param[1]
return addCM
class prover:
def commit(self, param, x):
q,g,h = generate(param)
r = number.getRandomRange(1, q-1)
c = (pow(g,x,q) * pow(h,r,q)) % q
return c, r
security = 80
msg1 = 1
msg2 = 2if (len(sys.argv)>1):
msg1=int(sys.argv[1])if (len(sys.argv)>2):
msg2=int(sys.argv[2])v = verifier()
p = prover()param = v.setup(security)c1, r1 = p.commit(param, msg1)
c2, r2 = p.commit(param, msg2)addCM = v.add(param, c1, c2)print "Msg1:",msg1
print "Msg2:",msg2print "\nc1,r1:",c1,r1
print "c2,r2:",c2,r2
print "\nWe can now multiply c1 and c2, which is same as adding Msg1 and Msg2"
print "\nCommitment of adding (Msg1+Msg2):\t",addCMresult1 = v.open(param, c1, msg1, r1)
result2 = v.open(param, c2, msg2 , r2)print "\nResult of verify c1:",result1
print "Result of verify c2:",result2result = v.open(param, addCM, msg1 + msg2 , r1, r2)print "Result of verify Msg+Msg2:",result
A sample run is [demo]:
p= 927367605776710231350038964859930613990112783097
q= 1854735211553420462700077929719861227980225566195
g= 587286479883053502476443629441944492972139657441
h= 1585397392778086356900624077167900433373970746021
Msg1: 10
Msg2: 100c1,r1: 689786752445290510488130348203999194170016173806 203870344555674172065766202773335149099800325291
c2,r2: 1285441962978034230356684788863924999023546017116 295304209484547410530265490717548256792202964716We can now multiply c1 and c2, which is same as adding Msg1 and Msg2Commitment of adding (Msg1+Msg2): 297081638871382420255252273169672989171885834401Result of verify c1: True
Result of verify c2: True
Result of verify Msg+Msg2: True
Perfect privacy
The Pedersen commitment can be seen as perfect privacy and where Eve cannot tell the value(s) that are contained in the commitment(s). In this case we have used discrete logs to implement the method, and in a future post I will show you how to use elliptic curves, with a blinding factor.
In a blockchain world, we could thus show our commitments to things on a blockchain, and then reveal our secret at some time in the future. This will be a world which has more trust, and which is focused on citizen’s rights and privacy.
My commitment …
Well, here is my commitment for a vote:
p= 1377860196042715093654767701692124472682331059357
q= 2755720392085430187309535403384248945364662118715
g= 2560750473692577537383174061148734042126729236716
h= 2572547898352324354720151290116424806302369392816
c1,r1: 1004101861002707610056229642851306235916375409356, 597268403498599198776838813357195563479826662181