The Beauty of Finding Prime Numbers

The Beauty of Finding Prime Numbers

You might not know it, but your core online security is dependent upon the magic of prime numbers. These special numbers are used in public-key encryption, such as for RSA and Elliptic Curve, and allow us to create puzzles which are easy to solve if you know a secret, but extremely difficult if you don’t know it. Overall we create a private key and a public key, and where we can sign (or encrypt) something with our private key, and then prove we have signed it with our public key.

The magic happens because of finite fields, and where we can mathematically operate on values using the mod of the prime number (mod p). And, so, these are all correct [demo]:

a (mod p) x b (mod p) = ab (mod p)
a (mod p) + b (mod p) = (a + b) (mod p)
a (mod p) — b (mod p) = (a — b) (mod p)

Where (mod p) is the remainder from an integer divide. Basically the (mod p) operation supports [here]:

Associate Law:
a+(b+c) (mod p)= (a+b)+c (mod p)
(a (b.c)) (mod p) = ((a.b) c) (mod p)

Commutative Law:
(a+b) (mod p) = (b+a) (mod p)
(a*b) (mod p) = (b*a) (mod p)

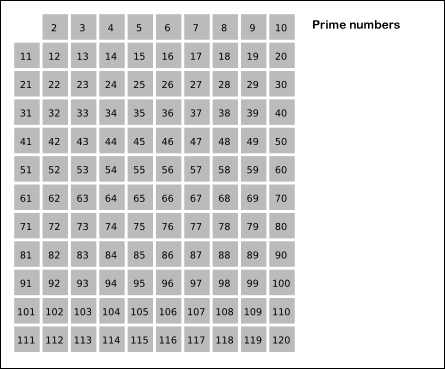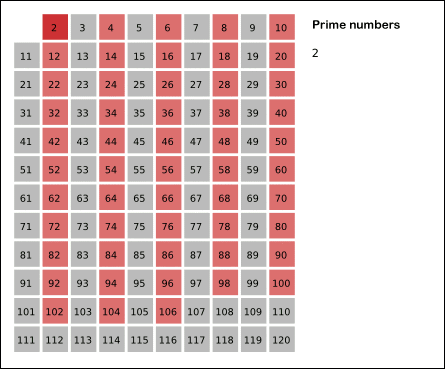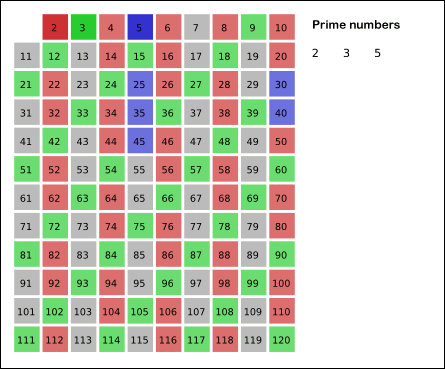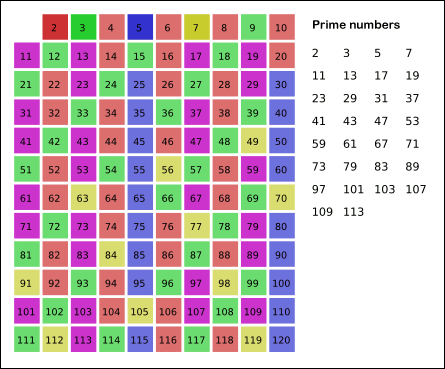
So, how can we search for prime numbers? Well, one of the most efficient ways to find all the prime numbers up to a given value is the sieve method — also known as the sieve of Eratosthenes. In this method, we lay out all the numbers from 2 onwards, and then take out multiples of 2, 3, 4, 5, and so on, until we are left with just the prime numbers:

Now, let’s create an efficient sieve in Python. We will start with a sequence of odd numbers (as we can automatically take these out), and then perform the same operation as above:

import sys

test=1000

if (len(sys.argv)>1):
	test=int(sys.argv[1])

def sieve_for_primes_to(n):
    size = n//2
    sieve = [1]*size
    limit = int(n**0.5)
    for i in range(1,limit):
        if sieve[i]:
            val = 2*i+1
            tmp = ((size-1) - i)//val 
            sieve[i+val::val] = [0]*tmp
    return [2] + [i*2+1 for i, v in enumerate(sieve) if v and i>0]
 
print sieve_for_primes_to(test)

This works because we start with all the odd numbers. If we have 100, then we will have 50 odd numbers. We start off with odd numbers in a sequence of:

3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 .. 99

In the first time round we have i equal to 1, and we will jump 3 each time and mark them as not prime:

3 5 7 -9- 11 13 -15- 17 19 -21- 23 25 -27- 29 31 -33- 35 .. 97 99

This takes out all the factors which are divisible by 3. In the next time around, we will jump 5, starting at 5 (and take out all the factors which are divisible by 5):

3 5 7 X 11 13 -X- 17 19 X 23 -25- X 29 31 X -35- .. 97 X

In the next time around, we will jump 7, starting at 7:

3 5 7 X 11 13 X 17 19 X 23 X X 29 31 X X .. 97 99

In the next time around, we will jump 9, starting at 9:

3 5 7 X 11 13 X 17 19 X 23 X X 29 31 X X .. 97 99

In the end, we stop at 19, and with a jump of 19, and add the value of 2 to the discovered prime numbers:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

The marking of the factors follows this sequence:

[1, 3, 5, 7, 9, 11,13,15,17,19,21,23,25,27,29,31,33,35 .. ]
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]
[1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0]

Here is the code running:

Conclusions

There you go, aren’t prime numbers magic?