Factoring with Elliptic Curve Methods

Factoring with Elliptic Curve Methods

One of the most interesting things I teaching and research into, is elliptic curve methods. While it is well known how we use elliptic curve methods for key exchange (ECDH) and with signature (ECDSA), it is less well-known that elliptic curve methods can be used to factorize values.

With this we basically compute kP (mod N), and where k is a product of many small numbers, such as Z!, and where we calculate one factor at a time. We could thus start with 2P, then use 3(2P), and then 4(3!)P, and then 5(4!)P, and so on. The value of Z is selected, so that the calculations are efficient on the curve.

If we move from a point P to 2P, we find the tangent to the point P and use this to find 2P. This tangent will be defined with a slope (s) and with a gradient in the form of ab. For this we must find the modular inverse of b. If we cannot find the modular inverse of b, a factor of N is gcd(N,b).

If our curve is y²=x³+ax+b, the slope (s) will be:

This is defined with differentiation. In detail, we first pick a random point P=(x0,y0) on an elliptic curve of:

We also select a random value of A and then calculate:

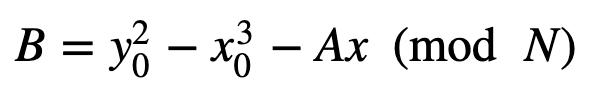
For two points on the curve: P=(Px,Py) and Q=(Qx,Qy), the slope of the line between them will be:

With this we have s in the form of ab(modN). Next we define:

and using:

If Px=Qx and Py=−Qy, we define as 0 [Identity], else we calculate R=P+P=2P=(Rx,−Ry):

Here’s a demo: