YAK … Authenticated Key Exchange

YAK … Authenticated Key Exchange

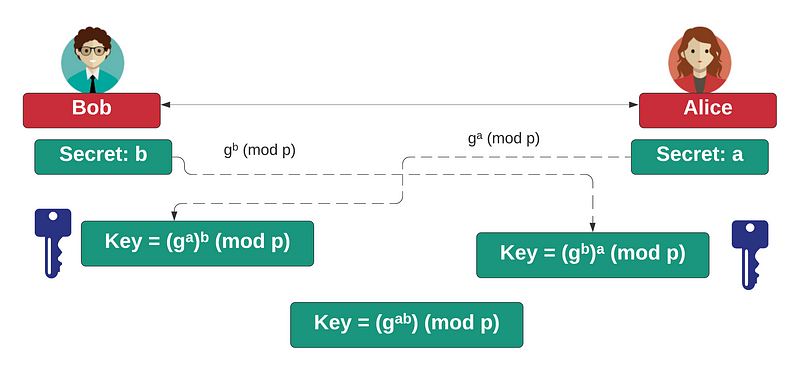
If you’re into Cybersecurity, you should hopefully all know about the magic of the Diffie-Hellman (DH) method. Basically, Bob and Alice agree on a generator (g) and a large prime number (p), and then Bob creates a secret (b), and Alice creates her secret (a). Bob then calculates B= g^b (mod p), and Alice calculates A=g^a (mod p). They pass their values, and Bob computes A^b (mod p) and Alice computes B^a (mod p) and they should end up with the same shared secret, and derive a secret encryption key for that:

The first time I saw this in action, and when I tried the numbers, I fell in love with the magic of cryptography. But there’s a flaw! What if Eve is in-between:

Now, Eve sits in the middle between Bob and Alice (‘a proxy’). Bob talks with Eve, and Alice also talks with Eve, and so we have a Eve-in-the-Middle. Bob has no way of knowing that he is talking to Eve instead of Alice, and the same goes for Alice. If Bob and Alice create a secure tunnel, Eve will decrypt things from Bob with K1, and then re-encrypt with K2 for Alice.

So how do we overcome this? Well, public key normally comes in somewhere, and where Alice and Bob can prove themselves using their public key. As a simple example we will take the YAK method, and which was defined by Feng Hao in 2010, and which focuses on authenticated key exchange (AKE) [here]:

With this method of AKE, Bob has a private key of b and a public key of:

Bpub=g^b (modp)

Alice has a private key of a and a public key of:

Apub=g^a (modp)

Just like with the DH method of key exchange, Alice generates a secret x and sends Bob:

A=g^x (modp)

For the key exchange, Bob generates a secret y and sends Alice:

B=g^y (mod p)

Alice computes:

K=(g^b g^y)^{x+a}(modp)

Bob computes:

K=(g^a g^x)^{y+b}(modp)

These values should be the same, as:

K=(g^b g^y) ^{x+a}(modp)=g^{(b+y)(x+a)}

Bob computes:

K=(g^a g^x)^{y+b}(modp)=g^{(a+x)(y+b)}

In this way, Alice will check Bob’s public key, and Bob will check Alice’s key, and only they will be able to create the secret key, as Eve does not have the required secret values that Bob and Alice have (their private keys: x and y). A demo using a 128-bit prime number is:

Prime:  215724695438718924354421417797563802497
g  2

Alice public key:  205412326610078321536315600196139515706
Bob public key:  179089747468154927852212148173309375757

Alice secret:	 17040461508873207
Bob secret:	 18678083293992335

Alice passes:	 19126688461477256476923071702392802133
Bob passes:	 91658868533302328032484343124318057321

Alice key:	 16102372395080110318170505028128817551
Bob key:	 16102372395080110318170505028128817551

Here is a demo:

and here is the code:

If you are interested, here is a P-AKE (Password Authenicated Key Exchange):