Lattice: The Easy and Hard Problem

Lattice: The Easy and Hard Problem

With lattice cryptography, we create a lattice of points and then introduce a small error in the point, and it then becomes a hard problem to find the nearest point to the point with the error.

Lattice cryptography is seen as a replacement for our existing public-key methods. What is so good about them, is that we have a provably hard problem. So, I’m going to show that this is a hard problem, and is based on this YouTube video [here]. In the presentation, we look at the CVP (Closest Vector Problem), and where we have we find the closest point. For simplicity we take two vectors (v_1 and v_2), and which connect from the origin to two points. We then find a solution for:

w = a(v_1) + b(v_2)

If v_1 and v_2 are orthogonal (they are almost at right angles to each other), Baini’s algorithm allows us to find the closest points, if not, we will get an incorrect answer. If we define one vector (v_1) with (5,1) and another vector (v_2) with (-2,8), we get the following lattice [here]:

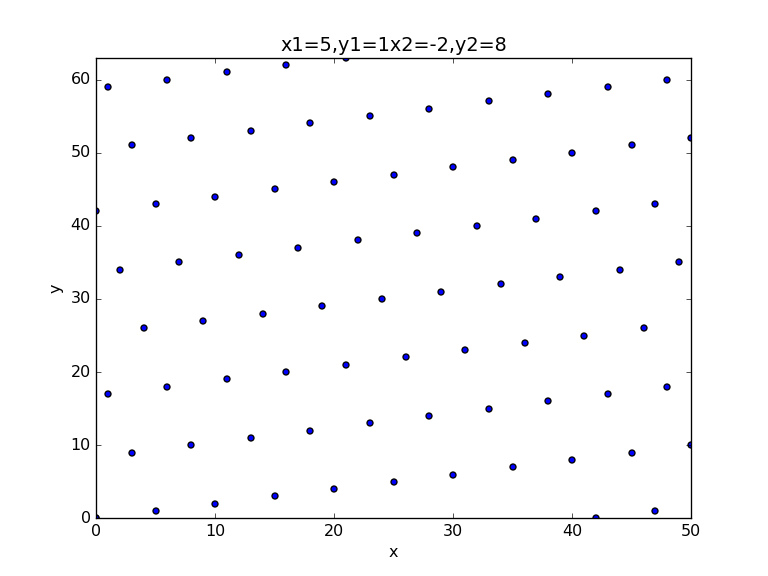
Now we want to find the nearest point to (27,8). First we determine if the angle between the points is around 90 degrees, and if it is, we should be able to solve for the nearest point using Babai’s algorithm:

We can now solve:

a 5 + b (1) = 27
a (-2) + b (8) = 8

For this we can solve the linear equation for a and b to get a=5.52 and b=0.309. This is then rounded to a=6 and b=0, to give a vector point of (30,6), and which is close to (27,8):

Cos theta: -0.04756514941544941
Grid point: 5 1
Grid point: -2 8
Solution (not rounded): 5.523809523809524 0.3095238095238095
Solution: 6.0 0.0
Nearest: 30.0 6.0

The Python code for this is:

import numpy as np
import numpy as np
import math
x1=5
y1=1
x2=-2
y2=8
x=27
y=8
costheta = ((x1*x2)+(y1*y2))/(math.sqrt(x1*x1+y1*y1)*math.sqrt(x2*x2+y2*y2))
print ("Cos theta: ",costheta)
print ("Grid point: ",x1,y1)

print ("Grid point: ",x2,y2)
_solve1 = np.array([[x1,x2], [y1,y2]])
_solve2 = np.array([x,y])
x = np.linalg.solve(_solve1, _solve2)
a=round(x[0],0)
b=round(x[1],0)
print ("Solution (not rounded): ",x[0],x[1])
print ("Solution: ",a,b)
print ("Nearest: ",x1*a+x2*b,y1*a+y2*b)
solx=x1*a+x2*bsoly=y1*a+y2*b

Now if we try two other vectors in the lattice of (37,41) and (103,113), the angle between them (Cos(theta)) is nearly zero, so we should not be able to solve:

In this case we get a solution of (-53,10), and which gives us an incorrect point of (-4,-26) and which is not near (27,8):

Grid point: 37 41
Grid point: 103 113
Costheta: 0.9999876301601318
Solution (not rounded): -53.0 19.0
Solution: -53.0 19.0
Nearest: -4.0 -26.0

We thus get the wrong answer, and this is what makes lattice crypto a hard problem. If we now try and solve for the point we found in the first part (30,6), we then get a correct solution for (37,41) and (103,113):

Grid point:  37 41
Grid point:  103 113
Solution (not rounded):  -66.0 24.0
Solution:  -66.0 24.0
Nearest:  30.0 6.0

So, we basically need to have orthagonal points on the lattice, and the solution becomes simple. Here is the code:

And here is a demo: