Secret Shares With Chinese Remainder Theory (CRT)

Secret Shares With Chinese Remainder Theory (CRT)
Asmuth–Bloom and Mignotte secret sharing using CRT
The general asked his army to arrange themselves into groups of 100, and the remainder was 25, then into groups of 101, and the remainder was 17, and then into groups of 102, and the remainder was 82. He announced that “We are 657,325 strong, let’s march! Here’s his solution:
With secret shares, we can take a secret, and then split it into a number of shares (n). Then we can define an algorithm to recover the secret using a threshold value (t). Thus we can split a secret in shares for Bob, Alice, Carol and Dave, and then define a thresold of three, so that Bob, Alice and Carol can come together with their shares and recover the value. Shamir used polynomials to share points, and where a curve can be recovered with enough points.
So let’s look at Shamir’s Secret Shares (SSS), and then look at regenerating with Chinese Remainer Theory (CRT). Both are defined as perfect secret sharing, as it should not be possible to regenerate the secret, without bringing together at least the number of shares defined by the threshold value.
Shamir’s Secret Shares
With secret sharing, we take a secret value and then share it with others. For example, we might have a share for Bob, Alice, Carol and Dave and then for three of them to come together to bring their shares together. First we generate a polynomial, and which has a secret value. In the following example, we have a quadratic equation of f(x)=2x² -2x + 5 [here]. The secret could be stored at f(0) (the red line), and where we give Bob the y value for x=1 (f(1) — the purple line), Carol the value at x=2 (f(2) — the blue line), Dave the value at x=3 (f(3) — the green line) and Alice the value at x=4 (f(4) — the outer blue line). With the values on their, they cannot recover f(0), but if we have three of the values, we can recover it:

For an any-3-from-4, we can use a quadratic equation, such as f(x)=20x²−2x+10, and where the value of 10 is the secret. Bob then gets the value of f(x) when x=1. This can be defined as f(1). Carol gets f(2), Dave gets f(3) and Alice gets f(4). The secret value is thus f(0). They then each know a point on the quadratic equation, and three of them can bring then back to recover the secret. In this case, we will generate a random polynomial of ax²+bx+secret, and then distribute the shares to Bob, Alice, Carol and Dave. Finally, we will recover the secret from three of these shares (Bob, Carol and Dave) [here]:
import numpy as np
import random
import sys
a = random.randint(20,20)
b = random.randint(-20,20)
secret = 10
if (len(sys.argv)>1):
secret=int(sys.argv[1])
seq = [a,b,secret]
f = np.poly1d(seq)
print ("Secret equation:\n",f)
print ("\nSecret: ",f(0))
print ("Bob: ",f(1))
print ("Carol: ",f(2))
print ("Dave: ",f(3))
print ("Alice: ",f(4))
x=[1,2,3]
y=[f(1),f(2),f(3)]
res=np.polyfit(x,y,2)
print ("\nSecret equation: ",res)
print ("Secret: ",int(round(res[2],0)))
The brilliance of the Numpy library comes to the fore here, as we can take a form of seq = [3,5,7] and generate a polynomial of 3x² + 5x + 7. A sample run with a secret of 10 and a secret equation of 20x²-19x+10 is [here]:
Secret equation:
2
20 x - 19 x + 10
Secret: 10
Bob: 11
Carol: 52
Dave: 133
Alice: 254
Secret equation: [ 20. -19. 10.]
Secret: 10
In this case, Bob, Carol and Dave bring their shares back to recover the secret. It is not possible for only two of them to recover the secret, as we need three points on a quadratic equation, to recover the equation. But, let’s say that Alice goes bad, and now Bob, Carol and Dave want to regenerate their secrets, without Alice getting involved.
Using Chinese Remainder Theory (CRT)
With Chinese Remainder Theory (CRT) we can solve for:
x=45 (mod 51)
x=14 (mod 41)
x=5 (mod 13)
In this case we find the value of x that will give a remainder of 41 when divided by 51, a remainder of 14 when divided by 41, and a remainder of 5 when divided by 13. Using Python we get:
from libnum import solve_crt
mod=[51,41,13]
rem=[45,14,5]
res=solve_crt(rem,mod)
print (res)
print (res % 51)
print (res % 41)
print (res % 13)
And where the result is:
96
45
14
5
The solution is thus x=96.
We can use the Chinese Remainder Theory (CRT) for secret shares. One method is the Asmuth-Bloom threshold secret share scheme [1]. For this, we create coprime integers (m_0,m_1…m_n), and have a secret (S). We then compute s_i=S+α m_0 (mod m_i). We can then bring together a number of shares and solve for CRT, as, for a threshold of three, we can solve:

to give a solution of:

and then taking:

will gives us S. The code is [demo]:
from libnum import solve_crt,generate_prime
from random import randint
import sys
bitsize=60
m=[0] * 5
share=[0] * 5
m[0]=generate_prime(bitsize)
m[1]=generate_prime(bitsize)
m[2]=generate_prime(bitsize)
m[3]=generate_prime(bitsize)
m[4]=generate_prime(bitsize)
m = sorted(m)
while ((m[1]*m[2]*m[3] < m[0]*m[3]*m[4]) and m[4]<m[3]):
m[4]=generate_prime(bitsize)
M=m[1]*m[2]
# for 3 from 4 we must have m1*m2*m3>m0xm3xm4
secret=5
if (len(sys.argv)>1):
secret=int(sys.argv[1])
alpha= randint(1, M)
share[0] = (secret+alpha*m[0]) % m[1]
share[1] = (secret+alpha*m[0]) % m[2]
share[2] = (secret+alpha*m[0]) % m[3]
share[3] = (secret+alpha*m[0]) % m[4]
print ("Secret: ",secret)
print ("Alpha: ",alpha)print ("\nPrime0: ",m[0])
print ("Prime1: ",m[1])
print ("Prime2: ",m[2])
print ("Prime3: ",m[3])
print ("Prime4: ",m[4])print ("\nShare 1 (s1,m1): ",share[0],m[1])
print ("Share 2 (s2,m2): ",share[1],m[2])
print ("Share 3 (s3,m3): ",share[2],m[3])
print ("Share 4 (s4,m4): ",share[3],m[4])
print ("Public part (m0): ",m[0])print ("\nNow using the first three shares and solve CRT")
mod=[m[1],m[2],m[3]]
rem=[share[0],share[1],share[2]]res=solve_crt(rem,mod) % m[0]
print ("Secret: ",res)print ("\nNow using the first two shares and solve CRT")
mod=[m[1],m[2]]
rem=[share[0],share[1]]res=solve_crt(rem,mod) % m[0]
print ("Secret: ",res)A sample run with a secret of 999, shows that we can recover the share with three shares but not with two shares [demo]:
Secret: 999
Alpha: 444245249422698541346812310673502438
Prime0: 650094581405656027
Prime1: 819353738310908587
Prime2: 906922952045910433
Prime3: 1040280684351465493
Prime4: 1138050480341993861
Share 1 (s1,m1): 354430321238022827 819353738310908587
Share 2 (s2,m2): 19078779414110362 906922952045910433
Share 3 (s3,m3): 912302619083664391 1040280684351465493
Share 4 (s4,m4): 546159951924698171 1138050480341993861
Public part (m0): 650094581405656027
Now using the first three shares and solve CRT
Secret: 999
Now using the first two shares and solve CRT
Secret: 448948650480899210
We share the public part m_0 with whoever will build the secret. The code is [demo]:
Mignotte threshold secret sharing
We can use CRT for secret shares. One method is the Mignotte threshold secret sharing [2]. For this we create co-prime integers for the number of shares (n) we need (m_0,m_1…m_{n-1}) and where:
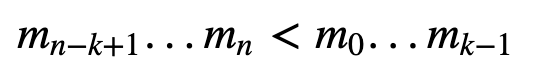
For co-prime, none of the values of m_i will share a factor. If they are all prime numbers, they will not share any factors. We make sure that:
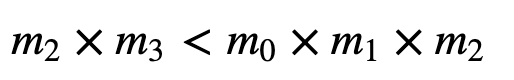
For example if, k=3 and n=4, we make sure that m2×m3<m0×m1×m2. We start with a secret (S) within a given range, and then compute the shares of:

We can then bring together a number of shares and solve for CRT. The code is:
# https://asecuritysite.com/encryption/sss_crt2?val1=999
from libnum import solve_crt,generate_prime
from random import randint
import sys
bitsize=60 # 60-bit primes
m=[0] * 4 # Array with five values
share=[0] * 4 # Array with five values
m[0]=generate_prime(bitsize)
m[1]=generate_prime(bitsize)
m[2]=generate_prime(bitsize)
m[3]=generate_prime(bitsize)
m = sorted(m)
while ((m[0]*m[1]*m[2] < m[2]*m[3]) and m[3]<m[2]):
m[3]=generate_prime(bitsize)
# for 3 from 4 we must have m0*m1*m2>m2xm3
secret=5
if (len(sys.argv)>1):
secret=int(sys.argv[1])
rand= randint(m[2]*m[3],m[0]*m[1]*m[2])
secret=rand+secret
share[0] = (secret) % m[0]
share[1] = (secret) % m[1]
share[2] = (secret) % m[2]
share[3] = (secret) % m[3]
print ("Secret: ",secret)
print ("\nPrime0: ",m[0])
print ("Prime1: ",m[1])
print ("Prime2: ",m[2])
print ("Prime3: ",m[3])print ("\nShare 1 (s1,m1): ",share[0],m[0])
print ("Share 2 (s2,m2): ",share[1],m[1])
print ("Share 3 (s3,m3): ",share[2],m[2])
print ("Share 4 (s4,m4): ",share[3],m[3])
print ("\nNow using the first three shares and solve CRT")
mod=[m[0],m[1],m[2]]
rem=[share[0],share[1],share[2]]res=solve_crt(rem,mod)
print ("Secret: ",res-rand)print ("\nNow using the first two shares and solve CRT")
mod=[m[0],m[1]]
rem=[share[0],share[1]]res=solve_crt(rem,mod)
print ("Secret: ",res-rand)A sample run with 60-bit primes:
Secret: 573145165887294485616490175405566692787387450499289968
Prime0: 757959770631913757
Prime1: 863172167552175001
Prime2: 943433622614114917
Prime3: 1008828436269265511
Share 1 (s1,m1): 748494740768369398 757959770631913757
Share 2 (s2,m2): 706690164490024 863172167552175001
Share 3 (s3,m3): 291772956089299981 943433622614114917
Share 4 (s4,m4): 690231746071021246 1008828436269265511
Now using the first three shares and solve CRT
Secret: 5
Now using the first two shares and solve CRT
Secret: -573145165887294485241420322814546302198249471625984773
References
[1] Kaya, K., & Selçuk, A. A. (2007). Threshold cryptography based on Asmuth–Bloom secret sharing. Information sciences, 177(19), 4148–4160.
[2] Mignotte, M. (1982, March). How to share a secret. In Workshop on Cryptography (pp. 371–375). Springer, Berlin, Heidelberg.