Knowing Where You Have Been …

As A Researcher … You Have To Know Where We Have Been …

As a good researcher, you don’t just dwell on the current methods, you must know your horizon. But equally, you should know how we got to where we are. It is a timeline of discoveries and enhancement, each making something better. But that memory is important as you sometimes have to bring back methods from the past and try them with new challenges.

As a researcher, I love reading new papers, but I only love reading some of the classics of the paper. These papers were often true break-through, and are often much easier to read than the overblown papers of the current time. A great paper of the past often had just a few references and a very short abstract, and would probably struggle to get past reviewers these days looking for many citations, and complex representations of maths.

And so we have our “standard” digital signature methods that use RSA and Elliptic Curve techniques, but let’s dive into another one from the past: Feige-Fiat-Shamir:

On Page 10, we have:

So, let’s go ahead and implement it. The Feige-Fiat-Shamir signature uses two random prime values (p and q) and create a modulus (n). From this Bob creates a public key and a private key, and uses the private key to sign a message, and this is proven with the public key.

Key generation

Initially, we generate two prime numbers (p and q ). We then generate:

We then select k random numbers (s_1,s_2…s_k) and compute:

The public key becomes (v1,v2…vk) and the modulus (n) and the private key becomes (s1,s2…sk).

Signature generation

Now Bob wants to sign a message (M). First, he selects a random number:

Bob then computes u:

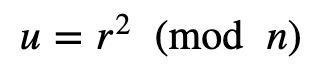
We can then compute the hash of the message and the value of u :

This gives us a bit array value of e_1,e_2,…e_k. Next, we compute the signature value:

Bob’s signature related to M is (e,s).

Verifying the signature

Alice computes:

The value of w should be the same as the value of u that Bob used. Alice can then easily compute the same hash as Bob with:

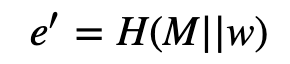
If the bit values of e and e′ match, the signature is valid. This works because:

And so u is equal to w, and thus e is equal to e′.

So here is the implementation:

and some code to prove that I’m not just outlining theory:

Conclusions

To understand where you are going, you need to understand where you have been. Go be a researcher …