Recovering a Message From a Signature

Recovering a Message From a Signature

Wouldn’t it be amazing, if you could sign for something, and the message you were signing for, was actually contained in your signature? Well, with the Nyberg-Rueppel method, we can do just now, and where Alice takes a message and then creates a signature. Bob can then check the signature, and recover the original message.

We normally use digital signatures to sign a message, and where the message is also defined alongside the signature. Alice will sign the message with her private key and then proves the signature with her public key. Within the Nyberg-Rueppel method we use ElGamal encryption, and can recover the message from the signature [here]:

In this case, the message is a value of 10, and we generate private and public keys of various sizes:

In ElGamal, we generate two prime numbers p and q and then make sure that q is a divisor of p−1. Next, we compute a value of α and with a generator value (g):

We then compute:

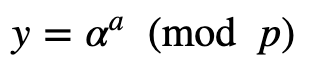
Alice’s public key is (y,α,p,q) and her private key is a. First, we compute:

and where R() is an affine method (m′=wm+a). Next, we generate a random value k and compute:

and:

The signature is then (e,s). Alice can send just the signature to Bob, and not the message. Bob then computes:

Finally, Bob does a reverse affine on this to recover the message:

The coding is here:

import random
import libnum
import sympy

from Crypto.Util.number import getPrime
from Crypto.Random import get_random_bytes

import sys
def affine(v,w,a,p):
  return((v*w+a) %p)

def affine_inv(v,w,a,p):
  return(( libnum.invmod(w,p) *(m_1-a)) % p)

primebits=32
w=3
a=7

if (len(sys.argv)>1):
  primebits=int(sys.argv[1])

if primebits>128: primebits=128

isprime=False

# For q, search for a prime q that is a factor of p-1

while (isprime==False):
  p = getPrime(primebits, randfunc=get_random_bytes)
  q = p//2
  if (sympy.isprime(q) and sympy.gcd(q,p-1)>1): isprime=True

alpha=3

a=random.randint(1,q-1)
y=pow(alpha,a,p)

m=10

m_1 = affine(m,w,a,p)

k = random.randint(1,q-1)

r=pow(alpha,-k,p)
e=m_1*r %p
s=(a*e+k) % q

print("\nMessage:")
print(f"m={m}")

print("\nAlice's private key:")
print(f"a={a}")

print("\nAlice's public key:")
print(f"p={p}, q={q}, alpha={alpha}, y={y}")

print("\nMessage Signature:")
print(f"e={e}, s={s}")

v=pow(alpha,s,p)*pow(y,-e,p)

m_1 = v*e % p

print (f"m_1={m_1}")

# libnum.invmod(e,PHI)

m = affine_inv(m_1,w,a,p)

print("\nCalculatioms:")
print (f"v={v}, m_1={m_1}")

print("\nRecovered message:")
print (f"m={m}")

A sample run is:

Message:
m=10

Alice's private key:
a=37737908942001075624479134056991415503

Alice's public key:
p=177624512367015397568242688683956241139, q=88812256183507698784121344341978120569, alpha=3, y=141633187385509314388948631189461294052

Message Signature:
e=9101952154582557625327758121489097638, s=43258691471757364317801777118231278593
m_1=37737908942001075624479134056991415533

Calculatioms:
v=23380663778044097971710542244000135145338381564564098978198735338337004922167, m_1=37737908942001075624479134056991415533

Recovered message:
m=10

and the code:

Reference

[1] Nyberg K, Rueppel RA (1995) Message recovery for signature schemes based on the discrete logarithm problem. In: De Santis A (ed) Advances in Cryptology — Eurocrypt’94, Lecture notes in computer science, vol 950. Springer, Berlin, pp 182–193 [here].