When Miller Met Rabin — Magic Happened …

When Miller Met Rabin — Magic Happened …

We live in a digitally flaw world. Very little of what we see can be truly trusted. But there are some people who have strived to make our world more trusted, and Michael O. Rabin is one of the most predominant. He was born in 1931 in Germany. In the 1960s he worked in the University of California and MIT, and then moved onto a Professorship at Harvard University. Finally, in 1981, he became a professor at the Hebrew University and has worked there ever since.

Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (n), we will have an odd number of (n−1), of which we can calculate the power of 2 with a value of s so that:

For example, if n is 25, (n−1) will be 24, and which is 2×2×2×3 and which is 2³×3. We then select a random value of a and which is between 1 and (n−1). We may have a prime if one of these is true:

and where r is a value between 0 and s−1. For example, if we take n=61, then (n−1)=60. This can be represented as: 2²×15, thus s=2 and d=15. Let’s select a=5, so we get:

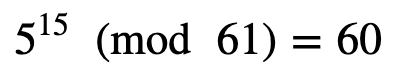
This does not pass the first test, so let’s try:

and which is equal to −1 (mod 61). It may thus be a prime.

Now we will try n=719 and where (n−1)=718. (n−1)=2×359, and thus s=1 and d=359. Let’s select a=7, and so the first test is:

This has worked, so it is a possible prime. Let’s not try a=9:

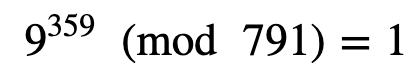
and so we have more proof of it being a prime number. The code is [here]:

import random
import sys
import libnum

 
n=97

if (len(sys.argv)>1):
	n=int(sys.argv[1])

a=random.randint(0,n)

res=libnum.factorize(n-1)

if n == 2: 
  print ("2")
  sys.exit()

if n % 2 == 0: 
  print ("Not prime")
  sys.exit()

print (f"n={n}\n")

s = 0
d = n-1
while True:
  quotient, remainder = divmod(d, 2)
  if remainder == 1:
    break
  s += 1
  d = quotient

r=s-1

print (f"(n-1)={n-1} = 2^{s} x {d}")

print (f"s={s}, d={d}")
print (f"a={a}, r={r}")

prime=False

if (pow(a,d,n)==1):
  print ("\nTest 1. It may be prime (a^d (mod n) = 1)")
  prime=True

if (pow(a,2**r*d,n)==(n-1)):
  print ("\nTest 2. It may be prime (a^{2^r d} (mod n) == n-1)")
  prime =True

if (prime==False): print("Not a prime")

A sample run with an unsafe value is:

n=31

(n-1)=30 = 2^1 x 15
s=1, d=15
a=3, r=0

Test 2. It may be prime (a^{2^r d} (mod n) == n-1)

Here are some tests using the M-R primality test:

• Is 5 prime?. Try
• Is 7919 prime?. Try
• Is 858,599,509 prime?. Try
• Is 982,451,653 prime?. Try
• Is 982,451,652 prime?. Try
• Is 643808006…,153 prime (210 digits)?. Try
• Is 643808006…,152 prime (210 digits)?. Try
• Is 4494179990..,163 prime (210 digits)?. Try
• Is 4494179990..,162 prime (210 digits)?. Try
• Is 23097…426570593 prime (210 digits)?. Try
• Is 23097…426570595 prime (210 digits)?. Try
• Is 5521712….5385789993 prime (220 digits)?. Try
• Is 56125680…531131327771 prime (230 digits)?. Try

Conclusions

Oh, go on … try your own example …