Two-pass Diffie-Hellman — MTI/A0

Two-pass Diffie-Hellman — MTI/A0, MTI/B0 and MTI/C0

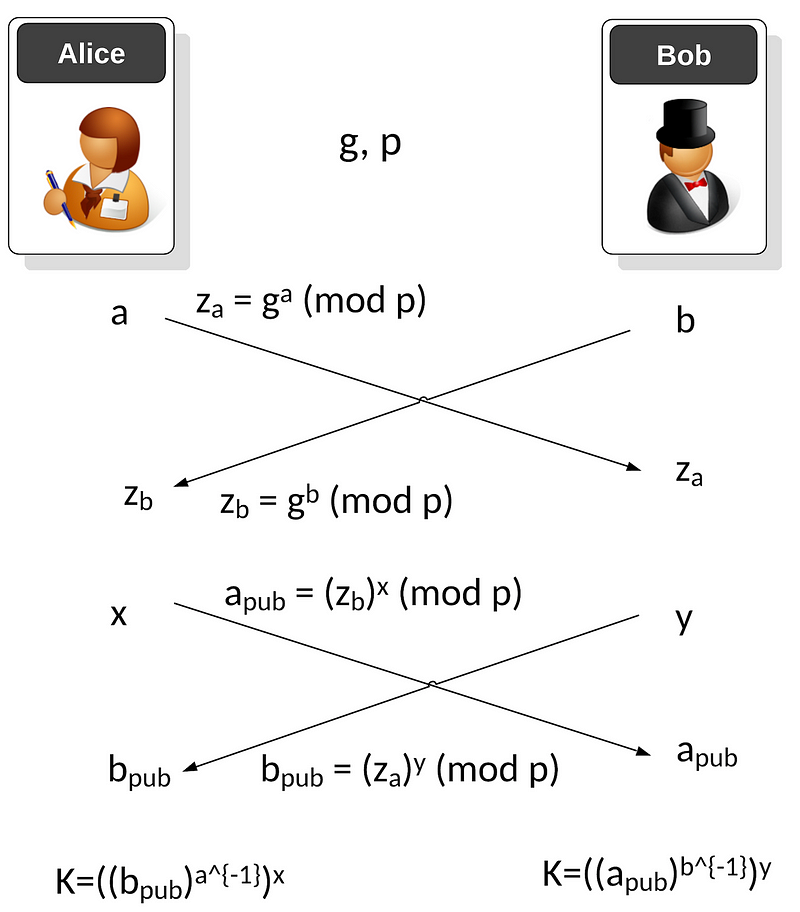
The Diffie-Hellman key exchange method is one of the great wonders of cybersecurity. It is simple, but it works so well. But, in its basic form it is weak from a security point-of-view, as Eve can perform an Eve-in-the-middle attack, as Alice does not authenticate the value received from Bob, and vice-versa. One way to overcome this is MTI/AO key agreement, and where Bob and Alice perform a trusted key exchange for a one-time setup. This passes z_a and z_b, and then each session passes public keys of a_pub and b_pub. An outline is:

The first phase is a one-time setup, and where Alice and Bob agree on a generator value (g) and a prime number (p). Next Alice generates a private key of a and Bob generates a private key of b. Alice then passes her public key of:

Bob passes his public key of:

When Bob and Alice want to generate a new key, Alice generates a random value x and Bob generates a random value y . Alice sends a public key value to Bob of:

Bob sends a public key value to Alice of:

Alice then generates a shared key of:

and Bob generates:

These will be the same as:

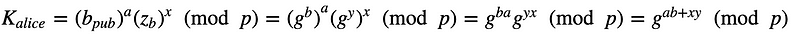
and Bob generates:

he following is the code [demo]:

import random

from Crypto.Util.number import getPrime
from Crypto.Random import get_random_bytes

import sys

primebits=32

if (len(sys.argv)>1):
  primebits=int(sys.argv[1])

g=3

p = getPrime(primebits, randfunc=get_random_bytes)

a=random.randint(1,p-1)
b=random.randint(1,p-1)

z_a = pow(g,a,p)
z_b = pow(g,b,p)

print(f"\nAlice's long term private key: {a}, long term public key: {z_a}")
print(f"\nBob's long term private key: {b} long term public key: {z_b}")

x=random.randint(1,p-1)
y=random.randint(1,p-1)

a_pub = pow(g,x,p)
b_pub = pow(g,y,p)

print(f"\nAlice's session private key: {x}, session public key: {a_pub}")
print(f"\nBob's session private key: {y}, session public key: {b_pub}")

K_a = (pow(b_pub,a,p)*pow(z_b,x,p)) % p
K_b = (pow(a_pub,b,p)*pow(z_a,y,p)) % p
print (f"\nAlice's Key:\t{K_a}")
print (f"Bob's Key:\t{K_b}")

And a sample run:

Alice's long term private key: 234922934927051736061407466859781671926, long term public key: 9553865896294691998820050822736010357

Bob's long term private key: 192684820488235721913538610637243476533 long term public key: 87629409173798051182302592765578727177

Alice's session private key: 176470342325955300772757080054933405845, session public key: 250928909289796421603126984483101721083

Bob's session private key: 217073041510159575168982756664701598050, session public key: 61705912907138968438256620254966595320

Alice's Key:	267734767508402112601722397616524910297
Bob's Key:	267734767508402112601722397616524910297

MTI/B0

The MTI/B0 has slight different approach, and where Alice create her public key for the session using Bob’s public key, and raising this value to her x value:

The implementation is here:

MTI/C0

The MTI/B0 has slight different approach, and where Alice create her public key for the session using Bob’s public key, and raising this value to her x value, but in this method we raise to the secret value (rather than multiplying by the public key value):

The implementation is here:

And for MTI/C1:

Conclusions

Here’s the demo for MTI/A0

and for MTI/B0:

and for MTI/C0:

and for MTI/C1: