How Do I Prove I Know The Answer to x²-x-42, Without Giving You The Answer?

We give away too much of our data. Why should we give away our password every single time that we log into a system? Why can’t we just…
Photo by Antoine Dautry on Unsplash

How Do I Prove I Know The Answer to x²-x-42, Without Giving You The Answer?

We give away too much of our data. Why should we give away our password every single time that we log into a system? Why can’t we just prove that we still know it? Thus Victor (the verifier) can prompt Peggy (the prover) with a puzzle, and where she can show that she can solve it. This is the method that zero-knowledge proof (ZKP) uses to prove things. In this case, we will use the method used by zk-SNARKs to prove that we still know a secret. This method is used in blockchain methods to anonymise transactions.

Pairing-based cryptography

With pair-based cryptography we have two cyclic groups (G1 and G2), and which are of an order of a prime number (n). A pairing on (G1,G2,GT) defines the function e:G1×G2→GT, and where g1 is a generator for G1 and g2 is a generator for G2. If U is a point on G1, and V is a point on G2, we have the following rules:

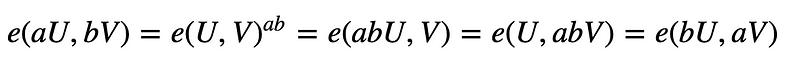
In this case, we will use pairing crypto to prove that we know the value of x which solves x²+ax+b=0. For example, if we have x²−x−42=0 has the solution of x=7 and x=−6 as (x−7)(x+6)=0.

First, we have two elliptic curves (G1 and G2). Crypto pairs can then be used to prove that Peggy still knows a secret. For this, we may have a quadratic equation of:

x²−x−42=0

Then, we will ask Peggy to prove that she knows the value of x. In this case, the solution is x=7 or x=−6. Now Peggy has to pass something to Victor to prove that she knows the solution, without giving away the value. For this, we have a point on an elliptic curve of G, and use the pairing property of:

and thus:

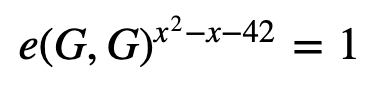
In pairing this then becomes:

and which becomes:

Peggy will then provide xG and Victor will check the pairings multiplied equals unity. In real-life x will be a large value, and it will not be possible to determine x from xG.

Coding

The outline coding using the library from the MIRACL library [here] is:

package main
import (
	"fmt"
	"github.com/miracl/core/go/core"
	"github.com/miracl/core/go/core/BN254"
	"math/rand"
	"time"
	"os"
	"strconv"
)
func Abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}
func FP12toByte(F *BN254.FP12) []byte {
	const MFS int = int(BN254.MODBYTES)
	var t [12 * MFS]byte
	F.ToBytes(t[:])
	return(t[:])
}
func randval() *core.RAND {
    s1 := rand.NewSource(time.Now().UnixNano())
    r1 := rand.New(s1)
    rng := core.NewRAND()
    var raw [100]byte
    for i := 0; i < 100; i++ {
       raw[i] = byte(r1.Intn(255))
    }
    rng.Seed(100, raw[:])
    return rng
}
func main() {
	x:=7
	a:=-1
	b:=-42
	argCount := len(os.Args[1:])
        if (argCount>0) {x,_= strconv.Atoi(os.Args[1])}
        if (argCount>1) {a,_= strconv.Atoi(os.Args[2])}
        if (argCount>2) {b,_= strconv.Atoi(os.Args[3])}
	G1:= BN254.ECP_generator() 
	G2:= BN254.ECP2_generator() 
	
	xG1:=G1
	xG2:=G2
 
	xGa:=G2 
	xGb:=G2 
	// Equ: x^2 + ax + b = 0
	if (x < 0) { 
		xG1 = BN254.G1mul(G1,BN254.NewBIGint(Abs(x))); xG1.Neg()
		xG2 = BN254.G2mul(G2,BN254.NewBIGint(Abs(x))); xG2.Neg()
	} else {
		xG1 = BN254.G1mul(G1,BN254.NewBIGint(x))
		xG2 = BN254.G2mul(G2,BN254.NewBIGint(x));
	}	
	if (a < 0) { 
		xGa = BN254.G2mul(G2,BN254.NewBIGint(Abs(a))); xGa.Neg()
	} else {
		xGa = BN254.G2mul(G2,BN254.NewBIGint(a)) 
	}
	if (b<0) { 
		xGb = BN254.G2mul(G2,BN254.NewBIGint(Abs(b))); xGb.Neg()
	} else {
		xGb = BN254.G2mul(G2,BN254.NewBIGint(b)) 
	}

	if (b < 0 && a < 0) { 
		fmt.Printf("\nEqn: x^2 - %d x - %d\n",Abs(a),Abs(b)) 
	} else if (b < 0) { 
		fmt.Printf("\nEqn: x^2 + %d x + %d\n",a,Abs(b)) 
	} else if (a < 0) { 
		fmt.Printf("\nEqn: x^2 + %d x + %d\n",Abs(a),b) 
	} else {
		fmt.Printf("\nEqn: x^2 + %d x + %d\n",a,b) 
	}
	fmt.Printf("\nxG1: %s\n",xG1.ToString()) 
	fmt.Printf("\nxG2: %s\n",xG2.ToString()) 
	fmt.Printf("\nxGa: %s\n",xGa.ToString()) 
	fmt.Printf("\nxGb: %s\n",xGb.ToString()) 

	pair1:=BN254.Ate(xG2,xG1);  pair1=BN254.Fexp(pair1)
	pair2:=BN254.Ate(xGa,xG1);  pair2=BN254.Fexp(pair2)
	pair3:=BN254.Ate(xGb,G1);  pair3=BN254.Fexp(pair3)
	fmt.Printf("\nPair 1 - first 20 bytes:\t0x%x\n",FP12toByte(pair1)[:20])
	fmt.Printf("\nPair 2 - first 20 bytes:\t0x%x\n",FP12toByte(pair2)[:20])
	fmt.Printf("\nPair 3 - first 20 bytes:\t0x%x\n",FP12toByte(pair3)[:20])
	pair1.Mul(pair2)
	pair1.Mul(pair3)
	fmt.Printf("\nPair Result - first 20 bytes:\t0x%x\n",FP12toByte(pair1)[:20])
	if (pair1.Isunity()){  fmt.Printf("\n\nYou have proven you know the value of x") } else {
		fmt.Printf("\n\nYou have NOT proven you know the value of x") 
	}

}

A sample run is [here]:

x =  -6
Eqn: x^2 - 1 x - 42
xG1: (047551bec1e6c80724663110982520fe8c88db44a4d42397ac219a1098d2763b,22936568b0f9da59025efcca3cbf0d40621e23ebd942985af7d213dcb427a922)
xG2: ([1ce69dc8742f5bb8a732dfe653515a23347fabdb638b00576008db7cb187f95a,01f33ef07a1fc794b14791741384fc9d0fcbe6abfa3570a374a8fb17d23657ed],[0b07db18cf5c53ba0897aedd52a96c638f466da17188b24ae0faf8011a0ff385,21bb29f6350e41819f2f1f959bde4decefed111f37767b5530cc898cf65f2adc])
xGa: ([061a10bb519eb62feb8d8c7e8c61edb6a4648bbb4898bf0d91ee4224c803fb2b,0516aaf9ba737833310aa78c5982aa5b1f4d746bae3784b70d8c34c1e7d54cf3],[230acce1d4506cbe1fa36ce996737de53763f5194241f6568d0f1f876e32d479,16683973c374eadb2ac709290a0c72d0b090f90028c636bc1cd2e51394c53178])
xGb: ([02347e5c2f0802a05e43267fe89de3dedc77d64556b495610913e6a767db7871,079078e9427f50798e62c1f804562a9326760f5d94f0a4206dd149d3f037d680],[0d250f7544ee22bc914c8d902b0a18c8a8613543217c01a07a3e73b380ddf93f,0c7cdecc7b14c33886d39fd4275f079c6a2d1639dc582262f231eece38b1987b])
Pair 1 - first 20 bytes:	0x006ce88251e092379d2d84308b8f76e908bf546e
Pair 2 - first 20 bytes:	0x05fb152b7cb6575543a9ac09ba4d8843da54f954
Pair 3 - first 20 bytes:	0x0b938a5c00b8130a459d660e1587afa15132a566
Pair Result - first 20 bytes:	0x0000000000000000000000000000000000000000
You have proven you know the value of x

If we try an incorrect value, such as x=5, we get a not proven result:

x =  5
Eqn: x^2 - 1 x - 42
xG1: (23edc69a751b579a14bc178029c6a6776a17fab345de03331bd905985b94daf0,215f727b315191c38806742b359c1aa7ebc35f65f5632eb8e9e6602f8890706b)
xG2: ([0b1d84f4d56634326a9c59f8161dd78be24b56b48a728012afea461f9191d674,21c158326bd5f7b921e22d5a528740d1fa40d4ad5924ab1d11c56a9f0a80b0c4],[0070bea4ee500dced8932db3b13554cdb986169e1a1180575562c32a6697afc4,20164c93784ca3c6b1db4fde1f24b8063a7a26b61ab465944ddffa3ce9cba6e5])
xGa: ([061a10bb519eb62feb8d8c7e8c61edb6a4648bbb4898bf0d91ee4224c803fb2b,0516aaf9ba737833310aa78c5982aa5b1f4d746bae3784b70d8c34c1e7d54cf3],[230acce1d4506cbe1fa36ce996737de53763f5194241f6568d0f1f876e32d479,16683973c374eadb2ac709290a0c72d0b090f90028c636bc1cd2e51394c53178])
xGb: ([02347e5c2f0802a05e43267fe89de3dedc77d64556b495610913e6a767db7871,079078e9427f50798e62c1f804562a9326760f5d94f0a4206dd149d3f037d680],[0d250f7544ee22bc914c8d902b0a18c8a8613543217c01a07a3e73b380ddf93f,0c7cdecc7b14c33886d39fd4275f079c6a2d1639dc582262f231eece38b1987b])
Pair 1 - first 20 bytes:	0x0992fbe1be5fa730dd57a1cb271d0b509d3bca98
Pair 2 - first 20 bytes:	0x2379e3f2a5512f8968af20800c70526b3a59897f
Pair 3 - first 20 bytes:	0x0b938a5c00b8130a459d660e1587afa15132a566
Pair Result - first 20 bytes:	0x0e7399bb64062eeab29b61a0067d9fd651f170b4
You have NOT proven you know the value of x

Now we can prove or not prove these:

  • x=-3, x²−2x−15. Success. Try!
  • x=5, x²−2x−15. Success. Try!
  • x=4, x²−2x−15. Failure. Try!
  • x=-15, x²+5x−150. Success. Try!
  • x=10, x²+5x−150. Success. Try!
  • x=-8, x²+5x−15 . Failure. Try!