The MVQ Method — Authenticated Key Exchange

The moment I understood the Diffie-Hellman method, was the moment I got into cryptography. When I learnt about RSA, I was so integreged by…

The MVQ Method — Authenticated Key Exchange

The moment I understood the Diffie-Hellman method, was the moment I got into cryptography. When I learnt about RSA, I was so intrigued by its simplicity and beauty. But the real inspiration came when I truly understood how elliptic curves. So I love implementing any related to the wonderful world of elliptic curves. So let’s look at an example.

MVQ (Menezes–Qu–Vanstone) was created Alfred Menezes, Minghua Qu and Scott Vanstone [1] in 1995 and is an authenticated key exchange method. It was integrated into the IEEE P1363 standard and uses points on an elliptic curve to generate a shared key. Overall Bob and Alice will hold a long-term key pair, and where these are then used to generate a shared session key.

Overall, Alice holds a key pair (A,a), and where a is Alice’s private key, and A=aG is her public key. For Bob, his public key will be B=aG and who has a private key of b. G is the base point on the elliptic curve.

We initially define a function of:

where:

In this case, n is the order of the elliptic curve, and where we have a point of R(x,y). We thus convert from a point (x,y) into a scalar value.

Alice creates a key pair (X,x) and where x is a private key value and X is a point on the elliptic curve (xG). Bob creates a key pair (Y,y) and where y is a private key value and Y is a point on the elliptic curve (yG). Alice determines:

and sends X to Bob. Bob determines:

and sends Y to Alice. Alice computes the shared key of:

Bob computes the shared key of:

This work because Bob calculates:

And Alice calculates:

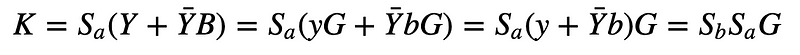
Coding

The following is the code [here]:

from secp256k1 import curve,scalar_mult,point_add
import random
from math import log10,ceil

print("Basepoint:\t", curve.g)

L = ceil(( (log10(curve.n)/log10(2)) + 1)//2)

a  = random.randrange(1, curve.n)
A = scalar_mult(a, curve.g)
b = random.randrange(1, curve.n)
B = scalar_mult(b, curve.g)

x  = random.randrange(1, curve.n)
X = scalar_mult(x, curve.g)
y = random.randrange(1, curve.n)
Y = scalar_mult(y, curve.g)

X_bar = (X[0] % pow(2,L)) + pow(2,L)
Y_bar = (Y[0] % pow(2,L)) + pow(2,L)

S_a = (x + X_bar * a) % curve.n
S_b = (y + Y_bar * b) % curve.n

print ("Alice a=",a)
print ("Bob=",b)
print ("x=",x)
print ("y=",y)
print ("L :",L)

print ("\nSa: ",S_a)
print ("Sb: ",S_b)

K1 = scalar_mult(S_a,( point_add(Y,scalar_mult(Y_bar,B))))
K2 = scalar_mult(S_b,( point_add(X,scalar_mult(X_bar,A))))

print ("\nKey (Alice):\t",K1[0])
print ("Key (Bob):\t",K2[0])

In this case we are using the secp256k1 curve. A sample run [here]:

Basepoint:   (55066263022277343669578718895168534326250603453777594175500187360389116729240, 32670510020758816978083085130507043184471273380659243275938904335757337482424)

Alice a= 40365018347807483701390957440210749090388911412345472561900697517743497889173
Bob= 50605843384046734317078854104654901306294380299043798609085054334527745441670
x= 78568539213960398121364802574408058020627778729352296557944114250026541109172
y= 11358446712949045291732139942330869107625036123262248924581447055611804923196
L : 128

Sa:  66703629997339194471255703264353989409749562821419127284203673589442147760745
Sb:  96743382205523597696252235026735397338778859858736349200451631881989301516359

Key (Alice):     58085126048856493761294920808153153533921328752368424169205674481895498811179
Key (Bob):   58085126048856493761294920808153153533921328752368424169205674481895498811179

The code is here:

Reference

[1] Menezes, A., Menezes, F. A., Qu, M., Vanstone, S., & Sutherland, K. J. (1995). Elliptic curve systems. In IEEE P1363, Part 4: Elliptic Curve Systems.