Conference Keying — From Napier’s Logs to Elliptic Curves

Conference Keying — From Napier’s Logs to Elliptic Curves

Discrete logarithm methods -such as with Diffie-Hellman — are not efficient these days as the prime number often has 2,048 bits or more. We thus focus more on elliptic curve methods, and which are much faster. The basics of them is to convert g^x (mod p) into xG, and where G is the base point on a curve, and x is the scalar. We thus perform a point multiplication rather than an exponential. When it comes to a multiplication, such as g^x g^y (and which is equal to g^{x+y}), we perform a point addition, such as xG + yG (and which is equal to (x+y)G). And that’s it, just two core operations: a point multiplication, and a point addition. So let’s convert a method which was defined in discrete logs as an elliptic curve method. For this we will use a conference keying method, and which will allow a number of conference participants to share an encryption key.

Burmester-Desmedt conference keying method

With conference keying, we have t participants, and each of these generates a secret value (r_i), and then transmit a public value generated from this (Z_i). Each of the participants then uses these values, and their secret value, and will generate the same secret key (K_i). In the following, we will use the Burmester-Desmedt method [1], and have five participants, and with varying sizes of a shared prime number (p), and for a common generator (g):

In the Burmester-Desmedt conference keying method, we have t users and then need to generate a common key (K):

First, everyone agrees on a prime number (p) and a generator (g). Next, for each participant i, each user generates a random number (r_i), and then compute a public value:

Each user then shares this value with the rest of the participants. Each participant then computes:

This is equivalent to:

Finally, each participant will compute the same key as:

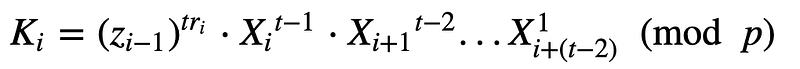
In the end, the key should be:

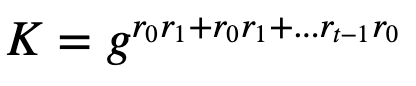
The coding is here:

import random
import sys
from Crypto.Util.number import getPrime
from Crypto.Random import get_random_bytesp=997
g=3
t=5primebits=64msg="hello"
if (len(sys.argv)>1):
  primebits=int(sys.argv[1])
if primebits>512: primebits=512p = getPrime(primebits, randfunc=get_random_bytes)z=[0]*t
X=[0]*t
r=[0]*t
K=[0]*tfor i in range(0,t):
  r[i] = random.randint(0,p)
  z[i]=pow(g,r[i],p)
  
for i in range (0,t):
  X[i]=pow(g,r[(i+1) % t]*r[i]-r[i]*r[(i-1) % t],p)
  
for i in range(0,t):
  K[i] = pow(z[(i-1) % t],(t)*r[i],p)
  for j in range(i+1,i+1+t):
    if (i==j): continue
    K[i]= (K[i]* pow(X[(j-1)%t],(t-j),p))% p
  print ("Keys:",K)res=r[0]*r[1]+r[1]*r[2]+r[2]*r[3]+r[3]*r[4]+r[4]*r[0]print ("Computing keys check: ",pow(g,res,p))

A sample run is:

Random values (r): [226589242101802, 189829639746726, 188625714155186, 184735699686400, 116440993319309]
Public values (z): [267704455905509, 50015333919247, 15916535078749, 264135697727188, 206738438540103]
X values: [112085216125079, 87590296821257, 260726071053053, 50830423926144, 23766863138958]Keys: [155751430205915, 155751430205915, 155751430205915, 155751430205915, 155751430205915]Computing keys check:  155751430205915

The code is:

From logs to elliptic curves

To convert to an elliptic curve method, we take the exponents and convert to point multiplication and take the multiplications and make then point additions. We have t users and then need to generate a common key (K). First, everyone agrees on the elliptic curve (secp256k1). Next, for each participant i, each user generates a random number (ri), and then compute a public value:

and where G is the base point of the curve. Each user then shares this value with the rest of the participants. Each participant then

Finally each participant will compute the same key as:

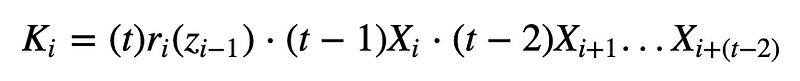
In the end the key should be:

The coding is here [here]:

import random

from secp256k1 import curve,scalar_mult,point_add

t=5 # Number of parties

z=[0]*t
X=[0]*t
r=[0]*t
K=[0]*t

for i in range(0,t):
  r[i] = random.randint(0,curve.n-1)
  z[i]=scalar_mult(r[i],curve.g)
  
for i in range (0,t):
  X[i]=scalar_mult( r[(i+1) % t]*r[i]-r[i]*r[(i-1) % t]  ,curve.g)
  
for i in range(0,t):
  K[i] = scalar_mult((t)*r[i],z[(i-1) % t])
  for j in range(i+1,i+1+t):
    if (i==j): continue
    K[i]= point_add(K[i],scalar_mult(t-j,X[(j-1)%t] ))
  

print ("Random values:",r)
print ("Public values:",z)
print ("X values:",X)

print ("\nKeys:",K)

res=r[0]*r[1]+r[1]*r[2]+r[2]*r[3]+r[3]*r[4]+r[4]*r[0]

print ("\nComputing keys check: ",scalar_mult(res,curve.g))

A sample run is [here]:

Random values: [4463755533774846637602847786757967242760690701307412228130857643967381735961, 96741168467817540081715654301555320158700388867341434828721393650453255123598, 61717472230239991980587257980114017418350116704648873039341165979823722071908, 31396563891021751196251791277695734072399130657200351619892753198581696606358, 94974630673319814151666749055588197124805370415672083005559727772301913543049]
Public values: [(90998925973083513632524330963385502701735581109878497335329151079303020577062, 70476537201409353199423621118851831820916810206517759824278218573427123274854), (102856868652781612746571171973939143500320236409384393268847771909963184530815, 13965495275489018774649599026486194870140041286252697791560233811209331936429), (99427446516467715961185033565252932237546785658238480036817281660874998037690, 82251641136334087997353903825716793391136726060564762099059018320882765839735), (16911560158753047673799685404669901591458309596275429611503718364197714304782, 98607243930441122214101848630482213064773819153199493507981140339018033703075), (80996244729840843346182126920131238615639835161760630079777852677521978441245, 96197448374393385713664339442731699552686581860563691777163087626748519797778)]
X values: [(100680773417056826796392972836368412942881478846041580947365227405336566099931, 81252703976782592443579928624901987165854250176997629439296479043515298170128), (16101859607536982072129354380897450431003353688964803707285331126652803561385, 112732197441811842906576112962764519089814958065782324313472455813793822069074), (15074040894883837781822534409993380373612978732311008136641548386000483940722, 109804456866678370366478104442243995459528193807709717970358142489076870096883), (22429915282361565376998416497359492372245028015609505651696750498280574308999, 72404092627159191603983409751568832688200126539081793183662988703011651518525), (97399537878596411031231666990291110758010935851808295555449530907457625436801, 97965381662004412161182160421748694350030391472605996320673526195132304679086)]

Keys: [(30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194), (30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194), (30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194), (30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194), (30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194)]

Computing keys check:  (30936135514666477810243436584887087257015238035391107280540936531549604687442, 69281525411964621344251301477793480609976500259298981379672706210590877300194)

The code is [here]:

Conclusions

Within conference keying, Eve sits and listens to Alice, Bob, Carol, Dave and Faith, and their broadcast values, but she cannot determine the shared key they will use for their secret communications. With elliptic curve methods, the maximum value we have is only 256 bits long, as, in sepc256k1, we use a prime number of 2²⁵⁵-19.

References

[1] Burmester, M., & Desmedt, Y. (1994, May). A secure and efficient conference key distribution system. In Workshop on the Theory and Application of of Cryptographic Techniques (pp. 275–286). Springer, Berlin, Heidelberg [here].