Koblitz and Miller Built The Foundation of Security For Our Internet

Koblitz and Miller Built The Foundation of Security For Our Internet

Your online security depends fundamentally on a beautiful little curve: an elliptic curve. It has been a savour of Cybersecurity in the face of ever-increasing key sizes for RSA, and weaknesses in discrete logarithms (as used in the Diffie-Hellman key exchange method). With RSA, we are moving to 2,048-bit key sizes, but with elliptic curve methods, our private key sizes are often just 256 bits long. For example, if you have Bitcoins, your private key which enables your owner of the cryptocurrency is just 256 bits long.

So I am so pleased that Neal I. Koblitz and Victor Miller were recently recognized for their work with the Levchin Prize at the real-world cryptography conference:

Both of them deserve the award as they discovered ECC independently of each other [1] here:

and [2] here:

Their idea came from preliminary work conducted by Lenstra on using elliptic curves to crack the RSA method:

Although they created ideas between 1985 and 1987, the main methods of ECC did not take off until 2005. The greatness of the method is the way we have scaled existing methods, such as the Diffie-Hellman methods, to ECDH (Elliptic Curve Diffie Hellman), and is almost a drop-in replacement. For digital signatures, the ECDSA (Elliptic Curve Digital Signature Algorithm) method has now been adopted as a standard for many applications, including for Bitcoin transactions. Overall, poor implementation has led to problems, such as the discovery of the private key through side-channel analysis, but these have been overcome based on Peter Montgomery’s work at Microsoft on the multiplication process:

Personally, I would say that elliptic curve cryptography is one of the most interesting areas of cybersecurity, so I’ve created my own examples here:

Elliptic Curve Cryptography

So what protects your privacy and security probably more than anything else on the Internet? That will be Elliptic Curve, and especially:

y² = x³+ax+b

where 4a³+27b² ≠ 0 (and which is needed to avoid singular points). The most popular curve is a Secp256k1 (or Curve 25519), and is defined with a=0 and b=7:

y² = x³+7 [Link]

In this, with ECC (Elliptic Curve Cryptography), we take a random number (n), and a point on the elliptic curve (G), and then multiply them together to produce P:

P = n G

G will be an (x,y) point on the curve that both Bob and Alice will agree to. n will then be Bob’s private key, and P will be his public key. The challenge is that if n is a 256-bit random value, it will be extremely difficult to find the value, even though we know G and P.

So let’s look at a bit of Python code in getting an elliptic curve setup:

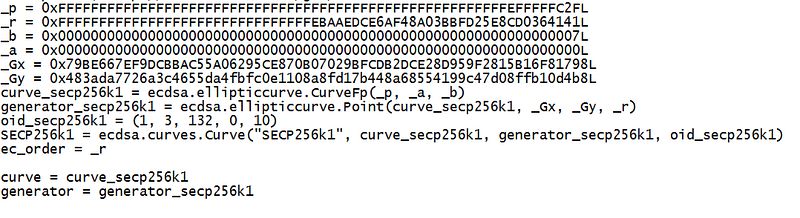
In this case, we see that _a is 0 and _b is 7 (y² = x³+7), and that we have a _Gx and a _Gy value. We also have _p which is a prime number in which all the operations are conducted with a (mod _p) function. In Python we could create two key pairs (one for Alice and one for Bob) with:

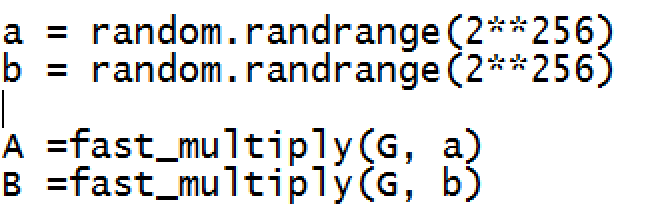
And where we generate a random 256-bit value for a, and then find the public key (A) by multiplying it with G. This will give us a point on the elliptic curve. Note that all of the operations are undertaken with (mod _p), and where the mod operator is the remainder of an integer division.

Analysing the keys

When we generate our key pair with Openssl, we see a 256-bit private key (and made from 32 bytes), along with a 65 bytes of a public key. The 04 at the start of the public key is an identifier. There are two 256-bit points that define the public key (and each is 32 bytes long):

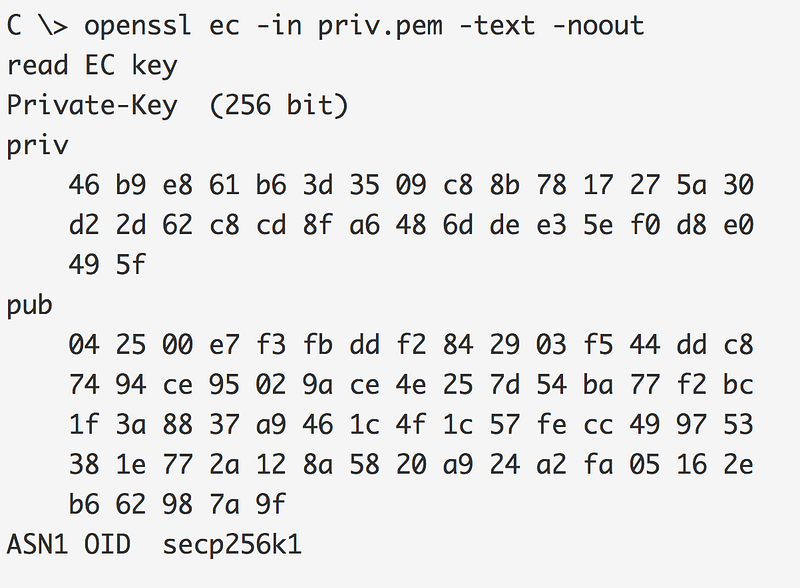
In this case the private key is:

and the public key:

The elliptic curve parameters that are shared can be viewed with:

Notice that the values here for the Prime, A, B and Generator and the same as the values for _p, _a, _b, _Gx and _Gx from the Python snippet above, and will are likely to be the same for any applications of this curve standard. If you are interested, some standards for curve parameters are defined here.

ECC Applications — Digital Signatures and Key Exchange

The two main applications of ECC are in digital signing and in key exchange. Within key exchange, we can take a similar method to the commonly found Diffie-Hellman method: ECDH. With this Bob and Alice both generate their key pairs and then exchange their public key values. Next the multiply these by their own private keys, and they should end up with the same point. The x value of the point is often used as the shared value, and this can be used to generate an encryption key [Link][Real-life example]:

A simple example is [Link]:

Basepoint: (920 (mod 3851), 303 (mod 3851))
Alice’s secret key: 25720
Bob’s secret key: 15297
==========================
Alice’s public key: (1996 (mod 3851), 3624 (mod 3851))
Bob’s public key: (94 (mod 3851), 884 (mod 3851))
==========================
Alice’s shared key: (2636 (mod 3851), 3251 (mod 3851))
Bob’s shared key: (2636 (mod 3851), 3251 (mod 3851))
==========================
The shared value is the x-value: 2636

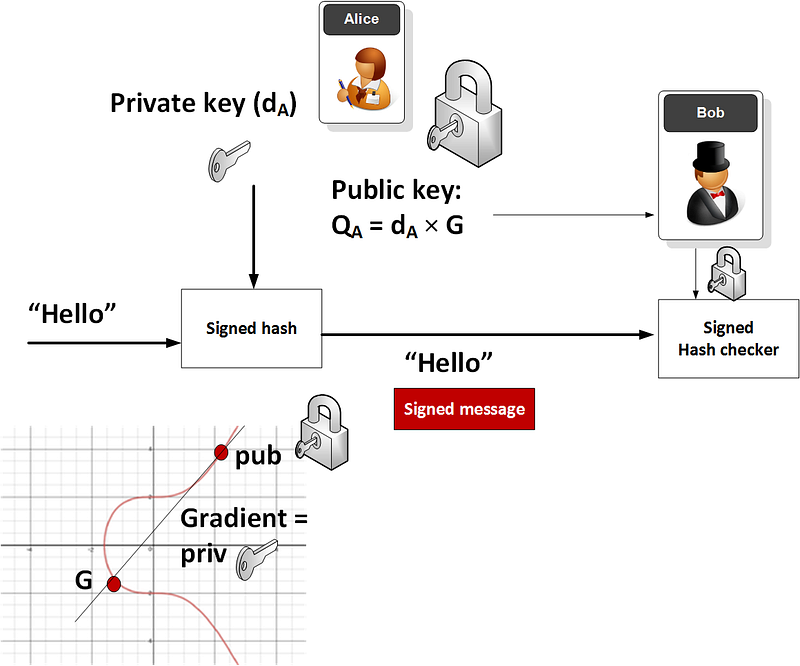
Another application of ECC is in signing, such as for Elliptic Curve Digital Signature Algorithm [here]. With this Alice will generate a key pair, and then encrypt the hash of a message with her private key. She then sends the message and the signed hash to Bob, who takes his own hash of the message, and decrypts Alice’s hashed version with her public key. If the hashes match, he has proven that Alice sent the message and that the message has not changed:

Bitcoin addresses and signing

Elliptic Curve is seen all over the Internet, smarts cards and in IoT applications. You can also see it with blockchain, where it is used as a standard method to sign transactions. With this Bob has a wallet, and which contains his public and private key. The private key is used to sign his transactions, and the public key will provide that he was the one that signed it. We also generate Bob’s ID from the key pair.

With this, Bob initially create a 256-bit value, and this will be his private key. The key is converted into a Base-58 form (and which gets rid of difficult characters such as ‘O’, and ‘l’ [here]). This is his WiF (Wallet Interchange Format) private key. He should not reveal this to anyone, and if possible should not store it on-line. Next, he will produce his 512-bit public key (as seen above). After this, it is then hashed with SHA-256 and RIPEM-160 to produce a public key hash value. This is then converted, using Base-58, into Bob’s Bitcoin ID:

And example of this is:

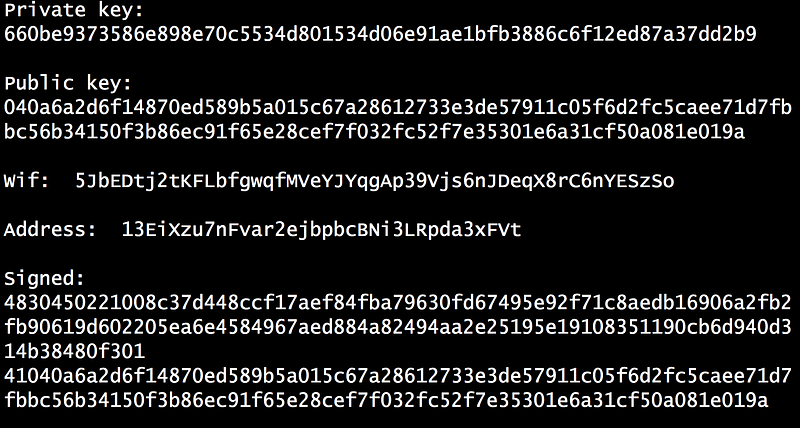
And so, it we want to send bitcoins to Bob, all we need to do is to get his address, and then sign a transaction with our public key.

Adding points

We have how we can multiply our points on the elliptic curve by a scalar value (our private key), but can we add our points? We if we take two points as:

P1 = n G

P2 = m G

If we add these points we get:

P1 + P2 = n G + m G = (n + m) G

Thus if we add the public keys (P1 + P2 (mod p)), the equivalent private key will be (n + m (mod p)). If Bob has a private key (a) and a public key (A), and then Trent has a private key (b) and a public key of (B). Then the public key will be A+B and the private key will be a+b. The following is an example [here]:

An application of this is where Trent produces a key which Bob can use to produce an equivalent key for the public keys produced:

Using fast_add() and fast_multiply() — taken from the Bitcoin library — we can implement this as:

A sample run is:

Key pairing over BN-curves

Elliptic curves are used fairly extensively in public-key encryption (such as in Bitcoin and Tor). A BN-curve (Barreto-Naehrig curve) [paper] defines an elliptic curve which can be used for pairings that allow for a high security and efficiency level. This page uses pairings over a 256-bit BN curve and derives a signature for a message. Elliptic Curve key pairing is also used with zk-SNARKs and zero-knowledge proofs. It can be used for “encrypted multiplication”.

For an Elliptic Curve we generate a 256-bit random number for the private key (p), and then take a point (G) [x,y] on the Elliptic Curve and then multiply it by the private key to get another point (p×x,p×y). In this way we get P=p×G, and where G is a known point on the Elliptic Curve, P is our public key and p is our private key.

With pairings, we can derive more complex relationships between the points, such as if P=G×p, Q=G×q and R=G×r, we can check to see if r=p×q, but where we only know P, Q and R (the public values). At the current time, we cannot compute pp from P=p×G, even if we know P and G. The exposure of the values is limited as we can calculate R=G×p×q , and where it is not possible to determine p or q.

The following code integrates the BN-256 code. Let’s test the code by simply creating a signature for a message. Bob will take a message and create a signature with his private key, and Alice will prove it with his public key.

First, we take the message and hash it to a point on the elliptic curve (pt). Next we take the private key (priv) — a random 256-bit value — and multiple the point to give priv×pt. This is the signature. Bob then generates his public key by multiplying his private key (priv) by G to give priv×G. Alice will then take the message and hashes it to a point on the elliptic curve (pt). Next, she multiplies this by Bob’s public key to get pub×pt . She also takes the signature (sig) and multiples it by G to get sig×G . If the signature is correct, the two values generated should match [here]:

Conclusions

ECC is magic! Try some here:

https://asecuritysite.com/ecc

References

[1] Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of computation, 48(177), 203–209.

[2] Miller, V. S. (1985, August). Use of elliptic curves in cryptography. In Conference on the theory and application of cryptographic techniques (pp. 417–426). Springer, Berlin, Heidelberg.