The Magic of Lattice and The Eye of a Falcon

The Magic of Lattice and The Eye of a Falcon

To understand lattice cryptography, you need to understand polynomials, as our bit values are converted into polynomials. Our operations are then conducted with polynomial multiplies and add, and taken with a (mod p) operation (and where p will be the maximum value we generate for the polynomial values). For example, to multiply (5x²+1) and (2x+3), we get:

10x³ + 15x² + 2x + 3

and if we had this with (mod 7), we would get:

10x³ + 15x² + 2x + 3 (mod 7) = 3x³ + x² + 2x + 3 (mod 7)

With lattice encryption, Bob and Alice agree to share N (the largest polynomial power), p and q. Bob generates two short polynomials (f and g), and generates his key pair from this. These polynomials have coefficients of -1, 0 and 1. For example:

We then should be able to calculate the inverse of f for (mod p) and (mod q). Thus:

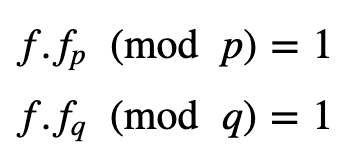
For example, if we use N= 11 and p= 31 and Bob picks a values of (f):

f=[−1,1,1,0,−1,0,1,0,0,1,−1]

We get:

and also picks:

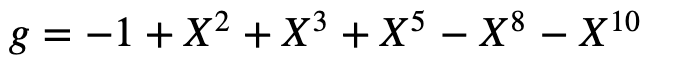
Using an inverse function we get [here]:

The public key then becomes:

and the private key is f and f_q. In this case we get [here]:

f_q . g: [-5, -9, -1, -2, 11, 12, 13, 3, 22, 15, 16, 29, 60, 19, -2, -7, -36, -40, -50, -18, -30]

We then divide by Z^N -1 and get:

H (Bob’s Public Key): [24, 19, 18, 28, 4, 8, 5, 17, 4, 17, 16]

And Bob’s private key is f and f_q. To encrypt we take Bob’s public key (h), a random polynomial (r) and a message (M), and then compute:

To decrypt, first we multiply by Bob’s private key f_q and take (mod q):

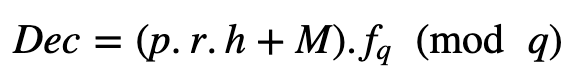
and which gives:

and since (fq.f)(mod q) is 1, we get:

Finally we multiply by fp (mod p):

This will be:

And since we have a multipler of p (mod p), we will get a zero value for the first term:

And since f.f_p (mod p) will be 1, we get:

Here is the complete working out for this example:

Falcon

The method we have defined here is known as NTRU (Nth degree TRUncated polynomial ring), and is one of the finalists for the NIST competition for post-quantum digital signatures. It is up against Falcon and CRYSTALS-DILITHIUM.

Falcon is actually derived from NTRU and is a lattice-based method for quantum robust digital signing. It is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler — Fast Fourier sampling. Some sample code for Falcon is [here]:

import falcon
import sys
import binascii

N=128
M="hello"
if (len(sys.argv)>1):
	M=str(sys.argv[1])
if (len(sys.argv)>2):
	N=int(sys.argv[2])

print ("Message: ",M)
M=M.encode()

sk = falcon.SecretKey(N)
pk = falcon.PublicKey(sk)
print ("Private key:",sk)
print ("Public key: ",pk)


sig = sk.sign(M)
print ("\nSignature: ",binascii.hexlify(sig))
rtn=pk.verify(M, sig)
print ("\nSignature verification: ",rtn)

A sample run of using an N value of 32 is:

Message:  Hello
Params:  {'n': 32, 'sigma': 154.6747794602761, 'sigmin': 1.1925466358390344, 'sig_bound': 1852696, 'sig_bytelen': 82}

Private key (f): [7, 21, -21, 13, 0, 5, 4, -4, -11, 16, 4, -10, 32, 29, -10, 16, -27, 8, 20, 2, 2, 45, 20, 7, -11, 8, 0, -11, 9, 31, 15, 6]
Private key (g): [-7, 14, 10, -3, 23, -1, 21, 7, -11, 9, -3, -3, -18, 6, 6, 2, -9, 4, -25, 15, 9, 4, 16, -15, 4, 34, 0, 2, 14, 10, 36, 0]

Private key (F): [0, -42, 52, 42, 5, 20, 20, 1, 10, -57, -39, 9, -25, 29, 32, -28, -2, -10, -12, -27, -34, -19, 25, -47, 17, 12, 2, -19, -19, -22, 40, 15]
Private key (G): [-8, -13, 23, -4, -17, 28, -11, 0, -5, -8, -12, -73, 32, 5, -14, 10, 32, -40, 52, -84, -37, 14, -5, 14, -28, 12, -10, -17, 43, -13, -7, -35]

Public key (n):  32
Public key (h):  [1963, 3496, 10854, 2667, 9364, 5962, 4641, 5262, 11809, 6207, 2827, 5191, 7644, 11634, 1835, 6, 9389, 854, 772, 11621, 3926, 401, 5324, 9751, 12110, 11105, 10216, 8785, 7072, 4246, 544, 7710]

Signature:  b'35b0406dbdd40dd178e5ad43f695b850d63241f79265697bbd4838927f9b2007e82220c7b0b38d3805d5cc782839b577c7a97cdefd8aebc4f5bed90fb5a5a4983ea96d2ec762738d59f7a5bc548f94000000'

and for N=128:

Message:  Hello
Params:  {'n': 128, 'sigma': 160.30114421975344, 'sigmin': 1.235926056771981, 'sig_bound': 7959734, 'sig_bytelen': 200}

Private key (f): [3, 9, 6, 17, 5, 9, 10, -2, 3, 0, -1, -6, -10, 3, -4, 2, 13, 2, -2, -14, 3, -16, 1, 3, -6, -14, 3, 1, 11, -10, 6, 0, 1, -3, -5, 4, -1, 2, -5, 9, -5, -3, 4, 12, -2, 13, 11, 3, -5, 8, -22, -3, 2, 11, 9, -3, 5, 7, -11, -3, 15, 4, -1, 0, 12, -4, 11, -4, -8, 3, 19, 5, 10, 2, 3, 2, 7, -13, -2, 6, -4, 2, 1, -5, -4, 2, 2, -9, 13, -7, 10, 0, 5, 6, -1, 10, 2, -10, 14, 2, -8, -8, 6, -1, -2, -3, 7, -5, 0, 2, -4, 11, -11, 2, 11, 3, 0, -3, 20, -9, 11, 2, 2, -9, -1, 0, 5, 2]
Private key (g): [-12, -3, -9, 9, 10, 4, 10, 4, 4, -7, 0, 11, 7, 7, 2, -3, -3, 3, -2, -9, 3, 15, -1, -4, 0, -10, 8, -4, 15, 3, 9, 5, 2, 0, 5, 2, 0, -4, 14, -7, 7, 3, -6, 6, 9, 5, -11, -12, 5, -1, -6, 14, -4, 10, 11, 4, -14, -4, 8, -3, -6, -5, 6, 12, -1, 0, 2, -15, 6, -4, 2, -18, 15, 17, -4, 14, -3, 2, -2, -5, -10, 3, 7, -4, -2, -7, -4, 6, -6, -3, -15, 14, 12, -4, 7, 9, -2, 13, 1, -9, 3, 2, 1, 11, 28, 16, -11, 3, 5, -9, 21, 11, 10, 6, -2, 11, -11, 3, 1, 6, -1, 4, 6, 1, -12, 14, 15, -10]

Private key (F): [-9, -36, -6, -3, 2, -9, 10, 25, 13, 26, 1, 46, -20, -17, -13, 15, 0, -16, 73, -10, 8, -21, -34, 7, 24, 34, -18, -12, -54, -17, -42, 47, -27, 46, 22, 9, 4, 18, 9, -46, -13, -7, 10, 23, 9, 26, 9, 54, -36, 14, 40, 21, -53, 35, 2, 1, 26, 28, 7, 6, 12, -1, -14, 21, 0, 16, -11, 12, -26, 21, 8, 13, 0, 0, 18, 60, 20, 49, 5, 25, -27, -12, -24, 2, -5, 26, -22, 6, -17, 2, -18, -10, 5, 2, 1, 15, -25, -7, -23, 17, 32, 48, 71, -3, 17, -39, 22, 37, -5, -27, -12, 12, -12, -27, 12, 4, 63, -26, 27, -23, 22, -5, 23, 4, 9, 17, 23, -37]
Private key (G): [-5, 18, 9, 19, 6, -28, -14, -19, -5, 14, -7, 39, 2, -8, -5, 26, -5, 39, -1, -6, 61, 14, -27, -38, 11, -28, -5, 26, 14, -27, -38, 14, -34, -3, 27, 52, -10, -3, -63, 14, -35, 5, 56, -14, 32, -11, 6, -68, -14, 15, -3, -15, 0, 21, -22, -10, -2, -26, 46, 32, 12, -26, 4, -5, -12, -7, 66, 5, -6, -3, -13, -26, 3, 41, -13, 12, 48, 27, 10, -36, 49, 2, 45, 5, 67, -25, -33, -13, -47, 9, 37, 51, -1, 17, 16, 15, -26, -18, 26, 11, 39, 4, 5, -5, 32, 52, 42, 24, 8, 43, -26, -36, 20, 44, 44, 50, 9, -27, 12, 41, -46, -76, 52, -4, 5, -39, -22, 3]

Public key (n):  128
Public key (h):  [1047, 4241, 11165, 10837, 1104, 6040, 2557, 10153, 5381, 6397, 9897, 5710, 2548, 5678, 11564, 4408, 2092, 10727, 337, 3253, 8390, 2944, 9337, 6943, 6370, 5782, 2721, 508, 3184, 9157, 12085, 2137, 10040, 978, 1052, 1658, 12018, 5832, 11191, 11022, 11674, 2286, 5559, 4138, 3113, 6198, 6700, 7863, 11052, 12286, 1002, 2786, 11385, 1384, 11477, 1240, 3835, 10122, 5671, 3242, 5387, 5701, 5866, 11823, 3903, 8336, 12051, 4013, 5772, 3500, 8756, 7402, 11361, 9301, 10169, 1527, 1315, 2712, 3873, 11584, 10823, 10545, 2009, 7368, 6375, 7578, 9572, 680, 1884, 3431, 4487, 11278, 11528, 10541, 2160, 1369, 3675, 6503, 11041, 10722, 8242, 4443, 5879, 10109, 8454, 1337, 8173, 8268, 4579, 5576, 9876, 6048, 9151, 1452, 12287, 10079, 7905, 1891, 805, 7106, 3141, 7108, 5461, 11325, 818, 8777, 6685, 8670]

Signature:  b'37e81845f909070a0637361d63653dd6a50277d496402c31f43107203b60e663e59fce86dda6be967a2d72a049b635af4f7b4efad522edd292b35ce95890c89e676ecce9a73016d620d1e7dd1f2927a365c5053daed75aad139ab0495c3884b8fbd26e9139713c9769db76f6434ae8523e3d948e1fcb9627bad793519667b7ce6898cbc8bc61d1bae5345025f972f3ea66d5586493db4270f17bc9c5bcc823bb2d231eaef1ceea531b3b982ad4a1178d3331dd84fd57357124ba3d295c5a46c8bd40000000000000'

Signature verification:  True

Conclusions

Say goodbye to RSA, Elliptic Curve and Discrete Logs, and say hello (possibly) to a Falcon.