Rainbow — The PCQ Oil and Vineger Method — Small Signatures, But Larger Keys (than Lattice)

Rainbow — The PCQ Oil and Vinegar Method: Small Signatures, But Larger Keys (than Lattice)
Here’s my 6 am doodles from this morning on multivariate cryptography:
Our existing methods of public-key encryption — such as discrete logs, RSA and elliptic curve — are known not to be a hard problem in a world of quantum computers. Multivariate cryptography is a known hard problem and is robust against quantum computers. Examples of methods that use multivariate cryptography are Oil-and-Vinegar, Unbalanced Oil and Vinegar, and Rainbow. While the original Oil-and-Vinger method has been cracked, we have advanced to Rainbow, and which is one of the finalists for the final round of the NIST competition for PQC (Post-Quantum Cryptography) signatures:

Multivariate cryptography
With multivariate cryptography, we have n variables within polynomial equations. For example, if we have four variables (w, x, y, z) and an order of two, we could have [here]:
w²+4wx+3x²+2wy−4wz+2wx+6xz=387
In this case, I know that the solution is w=7, x=4, y=5, z=6. For a matrix form, we could represent this as:

In order to constrain the values we get, we normally perform a (mod p) operation and where p is a prime number. This is known as a finite field, and our numbers are always constrained between 0 and p-1. For example, if we select p=97, we have:
w²+4wx+3x²+2wy−4wz+2wx+6xz=5 (mod 97)
Now there are multiple solutions to this now for w, x, y and z, so we define n multivariate polynomials. For example:
w²+4wx+3x²+2wy−4wz+2wx+6wx=96 (mod 97)
5w²+3wx+3x²+4wy−wz+8wx+4wx=36 (mod 97)
4w²+5wx+3x²+2wy−5wz+3wx+6wx=95 (mod 97)
6w2+7wx+4x2+2wy−8wz+2wx+9wx=17 (mod 97)
The solution to this is: w=7, x=4, y=5, z=6, but it is extremely difficult to solve, and know, and here is the code to prove this [here]:
import numpy as npp=97w=7
x=4
y=5
z=6def printM(M):
rtn = ""+str(M[0][0])+"w^2 + "+str(M[0][1]+M[1][0])+"wx + "+str(M[1][1])+"x^2 + "+str(M[0][2]+M[2][0])+"wy + "+str(M[1][3]+M[3][1])+"wz + "+str(M[0][3]+M[3][0])+"wx + "+str(M[1][2]+M[2][1])+"xz"
return rtnm=[w,x,y,z]
m_dash = np.transpose(m)
M0=[[1,2,1,1],[2,3,3,-2],[1,3,0,0],[1,-2,0,0]]
M1=[[5,2,1,2],[1,3,2,2],[3,2,0,0],[6,-3,0,0]]
M2=[[4,2,2,1],[3,3,3,-2],[0,3,0,0],[2,-3,0,0]]
M3=[[6,2,1,1],[5,4,3,-3],[1,6,0,0],[1,-5,0,0]]print ("m=",m)
print ("m^T=",m_dash)
print ("\nM0:",M0)
print ("M1:",M1)
print ("M2:",M2)
print ("M3:",M3)# res = m . M0 . m^{-1}
res1= np.dot(np.dot(m,M0),m_dash) % p
res2= np.dot(np.dot(m,M1),m_dash) % p
res3= np.dot(np.dot(m,M2),m_dash) % p
res4= np.dot(np.dot(m,M3),m_dash) % pprint ("Res0=",res1)
print ("Res1=",res2)
print ("Res2=",res3)
print ("Res2=",res4)print ()
print ()
print ("M0=",printM(M0))
print ("M1=",printM(M1))
print ("M2=",printM(M2))
print ("M3=",printM(M3))
and here is a sample run [here]:
m= [7, 4, 5, 6]
m^T= [7 4 5 6]M0: [[1, 2, 1, 1], [2, 3, 3, -2], [1, 3, 0, 0], [1, -2, 0, 0]]
M1: [[5, 2, 1, 2], [1, 3, 2, 2], [3, 2, 0, 0], [6, -3, 0, 0]]
M2: [[4, 2, 2, 1], [3, 3, 3, -2], [0, 3, 0, 0], [2, -3, 0, 0]]
M3: [[6, 2, 1, 1], [5, 4, 3, -3], [1, 6, 0, 0], [1, -5, 0, 0]]M0= 1w^2 + 4wx + 3x^2 + 2wy + -4wz + 2wx + 6xz
M1= 5w^2 + 3wx + 3x^2 + 4wy + -1wz + 8wx + 4xz
M2= 4w^2 + 5wx + 3x^2 + 2wy + -5wz + 3wx + 6xz
M3= 6w^2 + 7wx + 4x^2 + 2wy + -8wz + 2wx + 9xzRes0= 96
Res1= 36
Res2= 95
Res2= 17
The code is here:
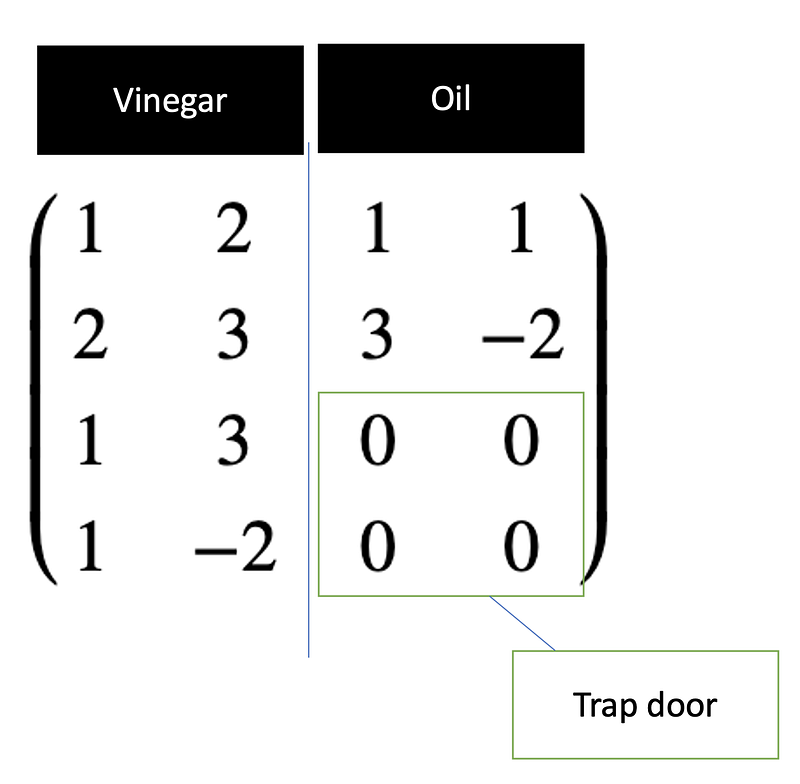
This matrix has a trapdoor, and where we define our vinegar and oil variables. The vinegar variables are secret and…asecuritysite.com
But, what good is this in solving things? Well, in the Oil and Vinegar method, we have a special trapdoor matrix, and which allows those with secret information to have privileged access to the usage of a public key and a private key. The matrices we defined early have the trapdoors built into them:
Practical implementation
Now let’s implement the method using the code used in the submission. The following is an implementation of Rainbow Classic [here]:
#include stdio.h
#include stdint.h
#include "rainbow_config.h"
#include "utils.h"
#include "rng.h"
#include "api.h"
#define MLEN 59
char *showhex(uint8_t a[], int size) ;
char *showhex(uint8_t a[], int size) {
char *s = malloc(size * 2 + 1);
for (int i = 0; i < size; i++)
sprintf(s + i * 2, "%02x", a[i]);
return(s);
}
int main(void)
{
size_t i, j;
int ret;
size_t mlen, smlen;
uint8_t b;
uint8_t m[MLEN + CRYPTO_BYTES];
uint8_t m2[MLEN + CRYPTO_BYTES];
uint8_t sm[MLEN + CRYPTO_BYTES];
uint8_t pk[CRYPTO_PUBLICKEYBYTES];
uint8_t sk[CRYPTO_SECRETKEYBYTES];
randombytes(m, MLEN);
crypto_sign_keypair(pk, sk);
crypto_sign(sm, &smlen, m, MLEN, sk);
ret = crypto_sign_open(m2, &mlen, sm, smlen, pk);
if(ret) {
fprintf(stderr, "Verification failed\n");
return -1;
}
if(smlen != MLEN + CRYPTO_BYTES) {
fprintf(stderr, "Signed message lengths wrong\n");
return -1;
}
if(mlen != MLEN) {
fprintf(stderr, "Message lengths wrong\n");
return -1;
}
for(j = 0; j < MLEN; ++j) {
if(m2[j] != m[j]) {
fprintf(stderr, "Messages don't match\n");
return -1;
}
}
randombytes((uint8_t *)&j, sizeof(j));
do {
randombytes(&b, 1);
} while(!b);
sm[j % (MLEN + CRYPTO_BYTES)] += b;
ret = crypto_sign_open(m2, &mlen, sm, smlen, pk);
if(!ret) {
fprintf(stderr, "Trivial forgeries possible\n");
return -1;
}
printf("CRYPTO_PUBLICKEYBYTES = %d\n", CRYPTO_PUBLICKEYBYTES);
printf("CRYPTO_SECRETKEYBYTES = %d\n", CRYPTO_SECRETKEYBYTES);
printf("CRYPTO_BYTES = %d\n", CRYPTO_BYTES);
printf("Signature Length = %d\n", smlen); printf("\nAlice Public key (only showing 1/512 of key): %s\n",showhex(pk,CRYPTO_PUBLICKEYBYTES/512));
printf("Alice Secret key (only showing 1/512 of key): %s\n",showhex(pk,CRYPTO_SECRETKEYBYTES/512)); printf("\nMessage: %s\n",showhex(m,MLEN));
printf("Signature : %s\n",showhex(sm,smlen)); printf("Verfied : %d\n",r);
return 0;
}A sample run of Rainbow Classic shows that the public key size is 161,600 bytes, the secret key is 103,648 bytes, and the digital signature of 125 bytes [here]:
CRYPTO_PUBLICKEYBYTES = 161600
CRYPTO_SECRETKEYBYTES = 103648
CRYPTO_BYTES = 66
Signature Length = 125
Alice Public key (only showing 1/512 of key): 7d3c1209d179008b11100d9674cb57474df22f356eaed1c28aa9da775a21b04b941654120768d8c02b0ec86480b00c97d044539677c9e67935d41c931ae77ed80a13ee4a734747b49bcfc2f9a76028d66a68ba69a2f48750ff3c7d830f8a1b545a9b9f0cc549b8601d02a8cebdb751c2525a5ddf5a928b34df01e114d74ae850a25d4ee4c5df7eb45ed23de1720961a75d01bcad44872be1d5f81e2e430ff77c1cbbc019507c0dae5702722ac4fb09681a328023d26852e0866b9808b0703de7ba89f0e6cbacff9edf9cbed446401c0724cf358878c3137dce0b48fa7bee9ff6132a6291ca030fbc1cc805f06a5d32fa2a1311afc44c0be748f0e955eba55ee06b536489f18240b2fba967ff6409227def9d496dc67eb3fce5bb79013fb7efdd3df4624feb764f3843809d9db0abd6b7a7fe676fd880277ce7390a
Alice Secret key (only showing 1/512 of key): 7d3c1209d179008b11100d9674cb57474df22f356eaed1c28aa9da775a21b04b941654120768d8c02b0ec86480b00c97d044539677c9e67935d41c931ae77ed80a13ee4a734747b49bcfc2f9a76028d66a68ba69a2f48750ff3c7d830f8a1b545a9b9f0cc549b8601d02a8cebdb751c2525a5ddf5a928b34df01e114d74ae850a25d4ee4c5df7eb45ed23de1720961a75d01bcad44872be1d5f81e2e430ff77c1cbbc019507c0dae5702722ac4fb09681a328023d26852e0866b9808b0703de7ba89f0e6cbacff9edf9c
Message: 530f8afbc74536b9a963b4f1c4cb738bcea7403d4d606b6e074ec5d3baf39d18726003ca37a62a74d1a2f58e7506358edd4ab1284d4ae17b41e859
Signature : 530f8afbc74536b9a963b4f1c4cb738bcea7403d4d606b6e074ec5d3baf39d18726003ca37a62a74d1a2f58e7506358edd4ab1284dbae17b41e8595820cceaf000a77c7f07cd79b579451e755754b052dfdc8748e88d7225dc508cf12ee2525cabb2ec3c0cad3575953a6f479bc1834cfe3d85430480ad9bb1a29903a9
The code is here [and here]:
The code compiles using the Makefile to “./rainbow-genkey”, and which is a Linux build. To run just run the executable:

Conclusion
The Oil and Vinegar method is my favourite technique in PCQ. It is unlikely to win the NIST competition for digital signatures, as lattice methods have smaller key sizes. For Rainbow we have:
CRYPTO_PUBLICKEYBYTES = 161600
CRYPTO_SECRETKEYBYTES = 103648
CRYPTO_BYTES = 66
Signature Length = 125
For Crystals Dilithum (Lattice) [here] we get:
CRYPTO_PUBLICKEYBYTES = 1312
CRYPTO_SECRETKEYBYTES = 2528
CRYPTO_BYTES = 2420
Signature Length = 2479
So, Rainbow wins on the digital signature size (125 bytes) and Crystals Dilithum wins for key sizes (1,312/2,528 bytes). I would be surprised if a lattice method didn’t win, but perhaps its small signature might win the day.
