In RSA, we have e, d, N, p and q, but what are dQ, dP and InvQ?

In RSA, we have e, d, N, p and q, but what are dQ, dP and InvQ?

In RSA, we would hope that many in cybersecurity would know that we generate two prime numbers (p and q), and then compute the modulus:

Then we pick an e value, and compute d from:

and where:

This gives us a private key of (d,N) and a public key of (e,N). We can then encrypt with:

and decrypt with:

But … when we view our key pair, we see three other values: dQ, dP and InvQ. What are these for?

Well, they relate to the Chinese theorem method for faster and less complex decryption. In the method, we do not have to perform the exponent for N, and only have to use exponents for p and q (and which are half the size of N). This makes the computation much faster and requires less complexity in the implementation. To compute the message, rather than computing:

we perform the following [here]:

c=pow(M,e,N)

m1=pow(c,dp,p)
m2=pow(c,dq,q)

h=(qinv*(m1-m2)) %p

m=(m2+h*q) % (N)

The following is the full code [here]:

from cose.keys.rsa import RSA
from cose.keys.cosekey import CoseKey
import binascii
from Crypto.Util.number import *

import sys

size=512
msg='hello'
if (len(sys.argv)>1):
 size=int(sys.argv[1])

if (len(sys.argv)>2):
 msg=str(sys.argv[2])

M=  bytes_to_long(msg.encode('utf-8'))

cose_key= RSA.generate_key(size)

print ("\ne=",binascii.hexlify(cose_key.e))
print ("n=",binascii.hexlify(cose_key.n))
print ("d=",binascii.hexlify(cose_key.d))
print ("p=",binascii.hexlify(cose_key.p))
print ("q=",binascii.hexlify(cose_key.q))
print ("dp=",binascii.hexlify(cose_key.dp))
print ("dq=",binascii.hexlify(cose_key.dq))
print ("qinv=",binascii.hexlify(cose_key.qinv))

e=int.from_bytes(cose_key.e,byteorder='big')
d=int.from_bytes(cose_key.d,byteorder='big')
p=int.from_bytes(cose_key.p,byteorder='big')
q=int.from_bytes(cose_key.q,byteorder='big')
N=int.from_bytes(cose_key.n,byteorder='big')
dq=int.from_bytes(cose_key.dq,byteorder='big')
dp=int.from_bytes(cose_key.dp,byteorder='big')
qinv=int.from_bytes(cose_key.qinv,byteorder='big')

c=pow(M,e,N)

m1=pow(c,dp,p)
m2=pow(c,dq,q)

h=(qinv*(m1-m2)) %p

m=(m2+h*q) % (N)

res=long_to_bytes(m)

print (f"\nc: {c} m1: {m1}, m2: {m2}, h: {h}, m: {m}")

print ("Decrypted: ",res.decode())

Notice that we now only have a multiplication and a modulus of N, rather than an exponential function. This makes the computation much less complex. A sample run gives [here]:

e= b'010001'
n= b'd973b230223a9304dab0bec08173aeea5fd1b42ca6c28814858d6ed65d5e4628f90063ebb5ffc3828a3c9472bb49a130dbd44c528f9441ac24787ee486dc7c65'
d= b'0bf02c22345ededf6f5a30bec4dca307bf06f64b55446cd0239ce62ee2a560589992e1325ac42fb3c84506b729a70a5fac742aafb884958472b5f6c428974ea9'
p= b'f7d767c413739f91be3d39f2a4a1e721f00b2121cc004441e59cdbe62fa0a30b'
q= b'e09c31b6ef5a045a1a10379f82ca296deb5ec9dd4a2c645e2239e099ebfa044f'
dp= b'6e7f6029204f058eb2159417656535aa80de45684f0eb35ff9e2447c4d31be5f'
dq= b'58901de624d058a0f25fec9ebfa258dd978e038876c3b43b8dc146774a9d856f'
qinv= b'8a1723d8f1f4f8ef8045c892508826bdc492467c5048216c81dbeda4863567a9'

c: 7223661198389890516329934575545958796298916087580560032777046876747271952396333920161885533505767897779796998857613544296539308995502046712937811568934017 m1: 448378203247, m2: 448378203247, h: 0, m: 448378203247
Decrypted:  hello

The value of dQ is:

and dP is:

and InverseQ is:

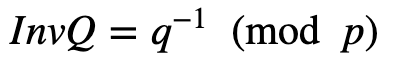
And there you go. A simplier decryption process. This is especially useful in IoT applications. If you are interested in this area, have a look at the COSE library:

https://asecuritysite.com/cose/

Subscribe: https://billatnapier.medium.com/membership