So What Is Lattice Encryption?

So What Is Lattice Encryption?

We live in an transistional world of digital trust. Why intermediate? Well, the core of the trust on the Internet is built around public-key encryption, and the core of this is at risk. Every time you connect to a Web site or create a secure connection, it is likely that public key encryption is defining the core trust of the connection and its security. For this we have a secret key (the private key) and a public key. The secret key is used to digital sign things and the public key is used to prove this signing, and link to the entity that signed it. While AES encryption may be doing the actual encryption of a secure connection, it is public-key encryption that is likely to be doing the key exchange and in checking the identity of the server.

But, what’s the problem? Well, quantum computers are able to crack our existing public key methods, including RSA, ECC and discrete log methods (eg Diffie Hellman key exchange). And so we need to find new methods to replace these, otherwise, our Internet will completely fail.

To plan towards the end of our public key methods, NIST has been assessing a range of techniques that cannot be cracked by quantum computers. These include lattice encryption (based on learning with errors), isogenies, Oil and Vinegar, and coding-based methods. While each has strengths and weaknesses, it is lattice encryption that leads the way in terms of key sizes, signature lengths, and computing time.

For public-key encryption, we need to replace two things: digital signatures, and key exchange/public key encryption. For a quantum robust version of digital signatures, the two main methods in NIST’s final list are: CRYSTALS-Dilithium [here]; and FALCON [here]. For key exchange/public key encryption they are: CRYSTALS-KYBER [here] and SABER [here].

The advantage of lattice in key exchange becomes obvious when you look at the size of the keys compared with McEliece (a code based method), and where the public key ranges from 800 to 1,568 bytes, but in the code-based method is rises to 1MB:

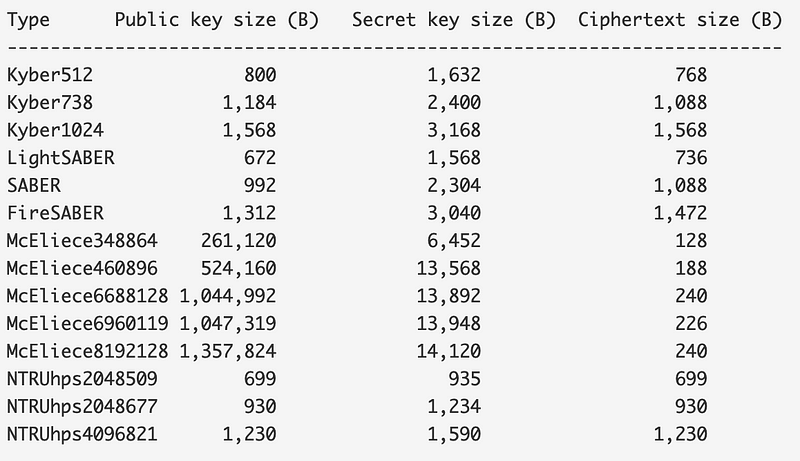
And for the actual generation of the keys, we can see that the number of CPU cycles for key generation, encapsulation (the process of converting the key into a form which can be received by the other side) and decapsulation (the process of converting the encapsulated form of the key into the required key) are so much faster than other competing methods:

If fact, McEliece is more than a thousand times slower in the above test run.

So how does it work? Well, have I created a whole lot of theory here. Basically, we have a multi-dimensional space and plot a grid of points that are equally spaced between each other. These points make vectors with the origin. The easy way to represent the vector of (5,6,7) is to use a polynomial, such as 7x²+6x+5. We can then operator on our vectors using polynomial operation. In Python, we can then apply add, multiply, subtract and divide operations for our polynomials:

print("\n== Operations ===")
print("A + B (mod p):\t",modPoly(addPoly(a,b),p))
print("A * B (mod p):\t",modPoly(multPoly(a,b),p))
print("A - B (mod p):\t",modPoly(subPoly(a,b),p))

print("\nUsing Polynomial notation")
print("a(x)=\t",Poly(a))
print("b(x)=\t",Poly(b))
print("p=\t",p)


print("\n== Operations ===")
print("A + B (mod p):\t",Poly(modPoly(addPoly(a,b),p)))
print("A * B (mod p):\t",Poly(modPoly(multPoly(a,b),p)))
print("A - B (mod p):\t",Poly(modPoly(subPoly(a,b),p)))

To constrain the sizes of the polynomial values, we use the (mod p) of a polynomial, and which constrains the factors to a value between 0 and p-1. An example, with a prime number of 17 is given next. In this case, the vector is (3,10,0,3,2) and represented by a=2x⁴+3x³+10x+3:

a(x)=    [3, 10, 0, 3, 2]
b(x)=    [4, 10, 0, 14, 0, 3]
p=   17

== Operations ===
A + B (mod p):   [7, 3, 0, 0, 2, 3]
A * B (mod p):   [12, 2, 15, 3, 8, 12, 4, 11, 9, 6]
A - B (mod p):   [16, 0, 0, 6, 2, 14]

Using Polynomial notation
a(x)=    2x^4 + 3x^3 + 10x + 3
b(x)=    3x^5 + 14x^3 + 10x + 4
p=   17

== Operations ===
A + B (mod p):   3x^5 + 2x^4 + 3x + 7
A * B (mod p):   6x^9 + 9x^8 + 11x^7 + 4x^6 + 12x^5 + 8x^4 + 3x^3 + 15x^2 + 2x + 12
A - B (mod p):   14x^5 + 2x^4 + 6x^3 + 16

With lattice encryption we use the learning with errors methods, and where we add a small error to the points. The task is then to find the close point to this point. If the lattice is large enough, this becomes a hard problem to solve. If we know a secret — our private key — it becomes easy.

If you want to know more about lattice encryption, try here:

https://asecuritysite.com/lattice

And here is an outline of how lattice encryption really works in practice:

Conclusions

Lattice methods will likely win both the key exchange and digital signature method in NIST’s competition. But one must worry about a weakness in the lattice approach being found, so there are a few alternatives that NIST are likely to propose, and one of these is isogenies. These involve two elliptic curves and define a mapping between them. If you are interested, try here:

https://asecuritysite.com/pqc/iso

One thing that is for sure, is that the migration has already started, with companies like Google, Amazon and Microsoft all making plans for a migration away from our existing public-key methods. While it might be 10 years in the future, we need to plan now, as we could rip up trust on the Internet, and reveal a whole lot of secrets. The Web we have is flawed, and mostly still based on the old protocols defined in RFCs, but the future will embed trust into every single operation, even down to the hardware level.