HVZK (Honest Verifier Zero Knowledge) For RSA and Using Kryptology

RSA is still a widely used public key method, but how do we get proof that the generation of the keys has been honest? And so I’ve been…
Photo by Joshua Hoehne on Unsplash

HVZK (Honest Verifier Zero Knowledge) For RSA and Using Kryptology

RSA is still a widely used public key method, but how do we get proof that the generation of the keys has been honest? And so I’ve been reading this paper to gain a method that can be used in Paillier and RSA to prove the validity of the keys generated [1][here]:

The focus of the paper is to prove that a suitable private key has been created, so that the public key has all the possible values within the given field, and without leaking anything about the private key. In RSA, we pick two large prime numbers (p and q)). We then calculate a modulus (N=pq) and ϕ(N)=(p−1)(q−1). We then make sure that gcd(pq,ϕ(N))=1. Along with this we select an e value for the exponation of the message:

C=M^e mod N

Normally e=65637. And so we need to provide proof of a safe modulus and the usage of e. Overall, Victor — the verifier — will not be able to factorize the modulus (N), so will have to trust Peggy in the creation of a secure modulus. For example, Peggy could cheat, and rather than creating N=p.q, she could create N=p.p, and which is p squared. This will produce a weak key. In the paper, the method to prove that the modulus is safe, along with the usage of e [here]:

In RSA, Peggy picks two large prime numbers (p and q). She then calculates a modulus (N=pq) and ϕ(N)=(p−1)(q−1). Now Victor wants Peggy to prove that she has produced a modulus which is safe and for the usage of e. For the proof Peggy computes:

In an interactive proof, Victor (the verifier) then generates a number of random values as challenges (x_i), and passes these to Peggy. She then computes:

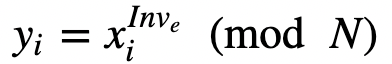
Peggy passes these back to Victor, and Victor then checks that:

for all values of i. If these are all true, Peggy has proven that the modulus is square-free, as she should not be able to generate the proofs if she has cheated. Overall, we can make this non-interactive (NI), by allowing Peggy the chance to create her own challenges, and then present these with the proofs.

The outline coding using the library from the Krytology library [here]:

package main
import (
 "crypto/rand"
 "fmt"
 "math"
 "math/big"
crypto "github.com/coinbase/kryptology/pkg/core"
)
func main() {
p, _ := rand.Prime(rand.Reader, 128)
 q, _ := rand.Prime(rand.Reader, 128)
 N := new(big.Int).Mul(p, q)
 PHI := new(big.Int).Mul(new(big.Int).Sub(p, big.NewInt(1)), new(big.Int).Sub(q, big.NewInt(1)))
PsfProofLength := 5
// 1. M = N^{-1} mod \phi(N)
 e := big.NewInt(65537)
 inv_e, _ := crypto.Inv(e, PHI)
// 2. Generate challenges
 x := make([]*big.Int, PsfProofLength)
 for i := 0; i < PsfProofLength; i++ {
  x[i], _ = rand.Int(rand.Reader, new(big.Int).SetUint64(uint64(math.Pow(2, 64))))
 }
proof := make([]*big.Int, PsfProofLength)
 // 3. Create proofs y_i = x_i^M mod N
 for i, xj := range x {
yi, _ := crypto.Exp(xj, inv_e, N)
  proof[i] = yi
 }
fmt.Printf("p=%s\n", p)
 fmt.Printf("q=%s\n", q)
 fmt.Printf("N=%s\n", N)
 fmt.Printf("\nChallenges:\t%v\n", x)
 fmt.Printf("Proof:\t%v\n", proof)
proven := true
 for j, xj := range x {
  // 4. Proof: yj^N == x mod N return false
lhs, _ := crypto.Exp(proof[j], e, N)
if lhs.Cmp(xj) != 0 {
   fmt.Printf("Failed at %d\n", j)
   proven = false
  }
 }
 if proven == true {
  fmt.Printf("\nZero knowledge proof of safe RSA\n")
 } else {
  fmt.Printf("\nNo Zero knowledge proof of safe RSA\n")
 }
fmt.Printf("\n\n== Now trying with an incorrect value of N ==\n")
N = new(big.Int).Mul(p, p)
proof = make([]*big.Int, PsfProofLength)
 // 3. Create proofs y_i = x_i^M mod N
 for i, xj := range x {
yi, _ := crypto.Exp(xj, inv_e, N)
  proof[i] = yi
 }
fmt.Printf("p=%s\n", p)
 fmt.Printf("N=%s\n", N)
 fmt.Printf("Challenges:\t%v\n", x)
 fmt.Printf("Proof:\t%v\n", proof)
proven = true
 for j, xj := range x {
  // 4. Proof: yj^N == x mod N return false
lhs, _ := crypto.Exp(proof[j], e, N)
if lhs.Cmp(xj) != 0 {
   fmt.Printf("[Failed at %d]", j)
   proven = false
  }
 }
 if proven == true {
  fmt.Printf("\nZero knowledge proof of safe RSA\n")
 } else {
  fmt.Printf("\nNo Zero knowledge proof of safe RSA\n")
 }
}

A sample run is [here]:

p=271417626796740746699456326017814174717
q=260044704350823857344471035007479473711
N=70580716515960694424313751868340354534468354367564794279878708532478962364787
Challenges: [3417249459559582116 1528534219686227524 7383391606638028962 9122092151467548878 6045045687018408321]
Proof: [1383764479771684498561367904817052143630982248698636062609989253492165926898 2848773332686650495449774176767240213078926974736321533249417367408944857428 48815209714888974163779050202021185965265967266443365508500534952861310063762 35192988639099586333461738676373671941986142170341357321112500750052090314697 23228528133624495555942078220937736819558370170060161459315330274192613937460]
Zero knowledge proof of safe RSA== 
Now trying with an incorrect value of N ==
p=271417626796740746699456326017814174717
N=73667528135974840648063360448081540482618825397132588160867164304847802030089
Challenges: [3417249459559582116 1528534219686227524 7383391606638028962 9122092151467548878 6045045687018408321]
Proof: [63166885033464814366069244801791755080711853832757030552408142059096391173887 60554031557934182305031755145915917550919633357595593133460180179163369290913 16018465568491358348967301720485164164657220811197620802893395277620940757603 31737272417688244036266455789384183282875703267741987201417344183206838765599 8987429795629908616603966345575612831407393041326381367610102628281519637069]
[Failed at 0][Failed at 1][Failed at 2][Failed at 3][Failed at 4]
No Zero knowledge proof of safe RSA

Conclusions

Who do you trust on the Internet? No one, basically. And so we need to create a proof of honesty. In this case, Peggy proves that she has created a valid RSA key pair. The zero-knowledge proof in this article thus allows Peggy to prove to Victor that she has been honest, and has generated the correct set of keys. She only has to do this one, of course.

If you are interested in Krytotology, try here:

https://asecuritysite.com/kryptology/

References

[1] Goldberg, S., Reyzin, L., Sagga, O., & Baldimtsi, F. (2019, December). Efficient noninteractive certification of RSA moduli and beyond. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 700–727). Springer, Cham.