From Smooth to Dot-to-Dot … Meet The Curve That Protects Your Online Security Like No Other
From Smooth to Dot-to-Dot … Meet The Curve That Protects Your Online Security Like No Other
You will find elliptic curves in so many areas of cybersecurity. In fact, the network connection you are using now is probably using them to generate the shared encryption key that your browser uses, and which is the same key that the same server. Everytime your connect, you both generate a new encryption key. We define this method as ECDH (Elliptic Curve Diffie Hellman).
For digital signatures, too, you’ll find them hard at work matching a user’s public key to a signature. In blockchain, Bitcoin and Ethereum use them as a core of their infrastructure, and where you’ll find the mighty secp256k1 curve. Two common elliptic curve signatures are ECDSA (Elliptic Curve Digital Signature Algorithm) and EdDSA (Edwards-curve Digital Signature Algorithm).
So let’s see how elliptic curves actually work. First, we start off with an elliptic curve equation of:

and where a and b are well-defined constants for our curve, and p is a large prime number (typically this has 256 bits, but can be larger). Overall a prime number of around 256 bits gives us around 128-bit security, which is more than enough for current security levels. There are another two parameters that we need. The first is the base point on the curve: G, and the second is the order of the curve (n). With G, we can perform operations relative to this point, so that Bob and Alice both know about G, and then could perform the same operations in relation to it. The order of the curve is the actual number of points we can use on the curve, and when we perform mathematical calculations on the curve, we perform them as (mod n). As so we have our curve:
Curve = (a, b, p, G_x, G_y, n)
and we are good to go. The secp256k1 curve is one of the most famous and used by Satoshi Nakamoti in defining Bitcoin. It has since been adopted by Ethereum. Other well well-known curves are [here]:
The number used in the curve name often gives away the size of the prime number used, and the larger the number of bits that the prime number has, the more security it is likely to be. So, P-192 has a 192-bit prime number, and P-512 has a 512-bit prime number.
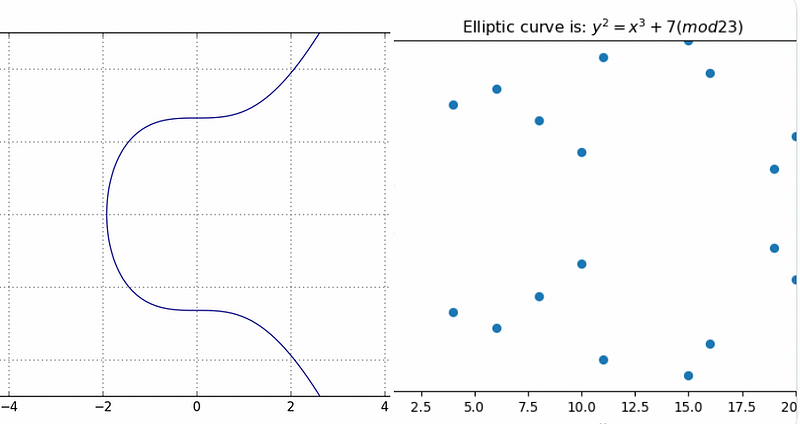
And, so we pick our curve, and Bob and Alice will use this. The diagram on the left in Figure 1 shows an example curve before the (mod p) operation, and the one on the right shows it after it [here].

The dots in the diagram on the right show that there are only two solutions to this for x=2:
y² = x³ + 7 (mod 23)
These are (4,18) and (4,5). So plugging-in x=2 gives:
18² = 4³ + 7 (mod 23)
5² = 4³ + 7 (mod 23)
If we run Python, we see that this is the case:

Overall, there isn’t a solution for every x co-ordinate, but where we end up with two possible points for every valid x co-ordinate. Obviously in real life, we are dealing with large numbers, which can be around 256 bits long.
The great thing about using the finite fields which are constrained with the prime number is that the rules that apply to our elliptic curves can still be applied within a finite field. So, we have a rule that when we add two points (P and Q) on an elliptic curve, we always get a valid point on the curve. Along with this, the point additional (P+Q) and doubling (2P) are efficient operations to compute. It is these two operations that make elliptic curve cryptography fairly fast in its operation.
And so, here’s the rest of the theory of how we use elliptic curves in public-key encryption:
And if you want to find out more about elliptic curve cryptography, try here: