Thank you to Adrien-Marie Legendre and Carl Gustav Jacob Jacobi for their symbols

In science, it is difficult to avoid Adrien-Marie Legendre, as there are so many things named after him: Fourier–Legendre series…
Adrien-Marie Legendre

Thank you to Adrien-Marie Legendre and Carl Gustav Jacob Jacobi for their symbols

In science, it is difficult to avoid Adrien-Marie Legendre, as there are so many things named after him: Fourier–Legendre series; Gauss–Legendre algorithm; Legendre chi function; Legendre duplication formula; Legendre–Papoulis filter; Legendre form; Legendre polynomials; Legendre sieve; Legendre symbol; Legendre transformation; Legendre wavelet; Legendre–Clebsch condition; Legendre–Fenchel transformation; Legendre’s constant; Legendrian knot; and Gamma function–Legendre formula.

And, so, where does Legedre help with your online security? Well, you will find his method used in elliptic curve methods, which are used to protect your online identity, and the security of the communications that you have with this Web page. So, let’s look at the Legendre Symbol.

Quadratic residues

Okay. Let’s say you want to determine the square root of 16. Well, that’s easy … as the answer is 4. But now, what is the square root of this:

6131408466595397710012614540363234062359700887928125190599453844504986420213585686778819217466610878266563405415556

Ans: 2476168101441297080746512578325117519920374855425678540834L

In a world of public-key cryptography, we often perform our operations within a finite field and use a prime number to define the finite field. Our operations are then undertaken with a (mod p) operation. Within elliptic curve methods, we define the curve as:

y² = x³ + ax + b (mod p)

and where we have our (mod p) operations. But if we calculate a point x on this curve, how do we find out if we have an integer value squared and (mod p)?

If we have the form of y²=a (mod p), we must find a value of y which results in a value of a (mod p). It is actually a difficult problem to solve. If a solution exists, the value of a is a quadratic residue (mod p). In modular arithmetic, this operation is equivalent to a square root of a number (and where x is the modular square root of a modulo p).

Legendre symbol

For this, we turn to Legendre who, in 1798, defined the Legendre symbol. In the following we will try and solve for the value of x, and also generate the Legendre symbol value [link]:

Solve x²=12 (mod 13)

With his method, we can determine that the answer is 8, as 64 (mod 13) is 12. Some sample code is [here]:

import sys
import libnum

def legendre_symbol(a, p):
    ls = pow(a, (p - 1) // 2, p)
    return -1 if ls == p - 1 else ls

n=11

if (len(sys.argv)>1):
  n=int(sys.argv[1])


print ("Here are the Z*p (quadratic residues modulo n and coprime to n):")

print ("\nJacobi symbol")

for a in range(1, n):	
  rtn= libnum.jacobi(a,n)
  if (rtn==1):
    print (a,end=', ')


print ("\nLegendre symbol")
for a in range(1, n):	
  rtn= legendre_symbol(a,n)
  if (rtn==1):
    print (a,end=', ')

A quadratic residue relates to the solving of the form: y=x² (mod n), and where we need to find values of y for different values of x, and for a given modulus (n). For n=11, we get Z∗p={1, 3, 4, 5, 9}. This is because, 1² (mod11)=1, 2² (mod11)=4, 3² (mod11)=9, 4² (mod11)=5, 5² (mod11)=3, 6² (mod11)=3, 7² (mod11)=5, 8² (mod11)=9, 9² (mod11)=4, and 10² (mod11)=1.

To find the quadratic residues for a given modulus, we can use the Jacobi symbol is:

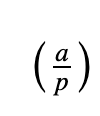
and is defined as:

The legendre_symbol returns:

  • 1. When a is a quadratic residue of p.
  • -1. When a is a quadratic nonresidue of p.
  • 0. When a shares a factor of p.

The Jacobi symbol was defined by Carl Gustav Jacob Jacobi as a generalized form of the Legendre symbol.

Elliptic Curves

While we have a trivial example here, we can use it for more complex ones, such as finding a point on the elliptic curve [here]. A sample run is:

Elliptic curve is:		P-192
Finding elliptic point closest to:	1
Prime number:			6277101735386680763835789423207666416083908700390324961279
a,b -3 2455155546008943817740293915197451784769108058161191238065
(2, 1126956676167578795924565825825899020268914906345645360775L)
(3, 2476168101441297080746512578325117519920374855425678540834L)
(5, 936760824408609109609580731987662341845728162027345586443L)
(6, 61374494507529673497365598443020935064779457192199494327L)
(8, 1539168359597512271047259505090133446672063593980132990812L)
(12, 3464753203279792192409824182683870253677262339932562461307L)
(13, 3288234558942609973454802567986887155175778959720199156770L)
(15, 4548834217212027584647316131131523554591911664904227806291L)
(17, 2148916484007672061843886225501299518817815267521173400039L)
(18, 1600977792967480259538850281480651298625682822208237361467L)
(22, 1682016893107185458056834822961338463540516386180178478778L)

The code for this is [here]:

import math
import sys
import libnum
def legendre_symbol(a, p):
    ls = pow(a, (p - 1) // 2, p)
    return -1 if ls == p - 1 else ls

def findit(start,p,a,b):
  x=start
  count=0
  while True:
    val=((x*x*x) + a*x+ b) % p
    rtn= legendre_symbol(val, p)
    if (rtn==1):
      if (libnum.has_sqrtmod(val,{p: 1})):
        res=next(libnum.sqrtmod(val,{p: 1}))
      print(x,int(res))
    count=count+1
    x=x+1
    if (count>20):
      return
    if (x-start>200):
      return
p = 2**256 - 2**224 + 2**192 + 2**96 - 1 
a=-3
b=41058363725152142129326129780047268409114441015993725554835256314039467401291
startval=1
type="P-192"
if (len(sys.argv)>1):
	startval=int(sys.argv[1])
if (len(sys.argv)>2):
	type=str(sys.argv[2])
if (type=="P-192"):
	p = 2**192-2**64-1
	a=-3
	b=2455155546008943817740293915197451784769108058161191238065
if (type=="P-224"):
	b=18958286285566608000408668544493926415504680968679321075787234672564
	p = 2**224 - 2**96 + 1 
	a=-3
if (type=="P-256"):
	p = 2**256 - 2**224 + 2**192 + 2**96 - 1 
	a=-3
	b=41058363725152142129326129780047268409114441015993725554835256314039467401291
if (type=="P-384"):
	a=-3
	b=27580193559959705877849011840389048093056905856361568521428707301988689241309860865136260764883745107765439761230575
	p = 2**384 - 2**128 - 2**96 + 2**32 - 1 
if (type=="Curve25519"):
	a=486662
	b=1
	p = 2**255 - 19 
if (type=="secp256k1"):
	a=0
	b=7
	p = 2**256 - 2**32 - 977 
if (type=="M-221"):
	a=117050
	b=1
	p = 2**221 - 3 
if (type=="BN(2,254)"):
	a=0
	b=2
	p = 16798108731015832284940804142231733909889187121439069848933715426072753864723  
if (type=="M-383"):
	a=2065150
	b=1
	p = 2**383 - 187 

print("Elliptic curve is:\t\t",type)
print("Finding elliptic point closest to:\t",startval)
print("Prime number:\t\t\t",p)
print("a,b",a,b)
findit(startval,p,a,b)

Conclusions

While cryptography seems so modern, the core methods it uses are often grounded in the work of individuals in the past.