Elliptic Curve Operations Within a Solidity Contract

Elliptic Curve Operations Within a Solidity Contract
Elliptic curve cryptography (ECC) operations are actually quite simple, and where we basically have a point add and a point multiply operation. With this we have a base point (G), and can then operate on this. So, let’s investigate using ECC operations on the Ethereum blockchain.
The code we will use is [here]:
This code can be added to Remix (here) and then compile the code:

This uses an external contract (EllipticCurve.sol) to implement the core functions. Next, we start Ganache as a local blockchain:
And then we deploy our smart contract to this blockchain:

Now let’s look at a few of the functions we have implemented.
Inverse Mod
With an inverse of a (mod p), we calculate a value (b) that will give:
(a x b) mod p = 1
In our smart contract, we have:
function invMod(uint256 val, uint256 p) pure public returns (uint256) {
return EllipticCurve.invMod(val,p);
}A sample run gives:

Thus the inverse of 19 (mod 997) is 105. We can prove that this is correct with:
(19 x 105) = 1995 = 1 (mod 997)
Modular Exponential
With a modular exponential, we compute:
a = b^c (mod p)
In our smart contract, we have:
function expMod(uint256 val, uint256 e, uint256 p) pure public returns (uint256) {
return EllipticCurve.expMod(val,e,p);
}If we try a sample run of b=65, e=101, and p=997, we get:

This works because:
a = 65¹⁰¹ (mod 997) = 1271302850988855649955877740540614892475208187760352651691755289585430714023709374227697793688402207534181186063394457937494576689321514086626098427590392248021089471876621246337890625 (mod 997) = 752
IsOnCurve
Now we will try the secp256k1 curve, and where the parameters are:
uint256 public constant GX = 0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798;
uint256 public constant GY = 0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8;
uint256 public constant AA = 0;
uint256 public constant BB = 7;
uint256 public constant PP =
0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F;
In the case we have a base point of (GX, GY), a prime number (p) of 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F, and:
y²=x³+7 (mod p)
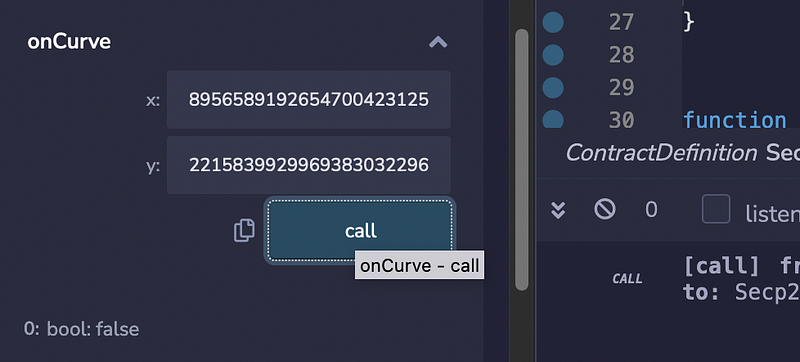
First, we can determine if a point is on the secp256k1 curve. Let’s take the point from here:
(89565891926547004231252920425935692360644145829622209833684329913297188986597, 12158399299693830322967808612713398636155367887041628176798871954788371653930)
This point represents 2G (or G+G). Let’s try it in our smart contract:

We can see if returns true, while if we add an incorrect point:
Recovering the y co-ordinate point
Within our elliptic curve, we have (x,y) points, but we do not actually have to store the y coordinate point, and only have to record its prefix. Now, let’s use the x coordinate value for 2G, and see if we can recover the y coordinate point:
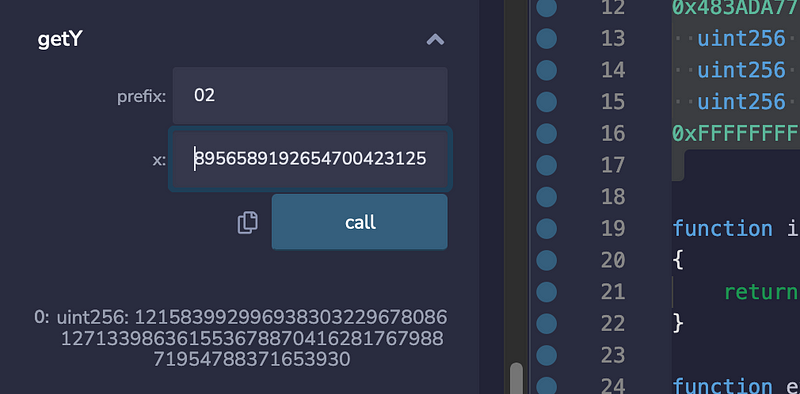
The result is 1215839929969383032 … 887041628176798871954788, and which is correct for 2G.
Inverse point
With ECC, we can have two points for every valid x co-ordinate value. Basically, the value is the negative value for the y coordinate point (and converted to an integer. In the following we determine the inverse of the 2G point we have previously used:

The inverse point is thus:
89565891926547004231252920425935692360644145829622209833684329913297188986597, 103633689937622365100603176395974509217114616778598935862658712053120463017733
Multiplying a point
With elliptic curve methods, we create a random value (n) for our private key, and then derive our public key value with:
Pub= n.G
and which is basically G added to itself n times. The code is:
function derivePubKey(uint256 privKey) pure public returns (uint256,uint256) {
return EllipticCurve.ecMul(privKey,GX,GY,AA,PP);
}Let’s take a value of n=2, and compute 2G:

We can see we derive the 2G point.
Point adding
One of the basic operations in elliptic curve cryptography is the adding of two points:
P = P_1 + P_2
Let’s add G and 2G:

In this case, we get 3.G, and we can check here:

Conclusions
And there you go … ECC operations on Ethereum. I have created a demo here: