Goodbye to Elliptic Curves? … Not, Quite … Here Come Isogenies

Goodbye to Elliptic Curves? … Not, Quite … Here Come Isogenies
The most interesting thing I have learn in the last few years is the theory of elliptic curves. How can something so beautiful as an elliptic curve be able to create unique encryption keys for Bob and Alice, and allow Alice to digitally sign messages? It is just pure cryptography magic! But, they have a fundamental problem, and it’s a big one … they can be cracked by quantum computers. So will we see the end of elliptic curves? Well, perhaps, but isogenies could see elliptic curves scale into a post quantum era. Let’s see if elliptic curves will live on in key exchange … with SIKE.
NIST PQC
Well, we are now at the final stage of NIST’s post-quantum cryptography standardization, and which started in 2016:

The finalists mainly include lattice-based methods. For key exchange/public key encryption we have: CRYSTALS-KYBER; NTRU; and SABER, and for digital signatures: CRYSTALS-DILITHIUM and FALCON. Only McEliece (for key exchange) and Rainbow (for digital signatures) make an appearance for non-lattice-based methods. Unfortunately, Rainbow has been cracked, so it will not win.
So it is likely that a lattice-based method will win, and become a standard. But what about the future? What if lattice methods are cracked? Well, NIST has a plan for this, and have defined a competition for alternative candidates. These candidates will be the backup route against the likely lattice method. And one area which shows the most promise as an alternative is isogenies. So let’s look at one of the most promising methods: SIKE. It has such potential that AWS has defined a standard for its integration into TLS 1.2 [here]:

SIKE
Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange and is based on Supersingular Isogeny Diffie-Hellman (SIDH). It has a similar methodology to the Diffie-Hellman method but is quantum robust. Overall it was created by Luca de Feo and David Jao [2][paper] and enhanced by Craig Costello, Patrick Longa, and Michael Naehrig at Microsoft [3][paper].

It has one of the smallest key sizes for quantum robust crypto methods (where the public key can be compressed to 378 bytes and with a private key of 434 bytes):
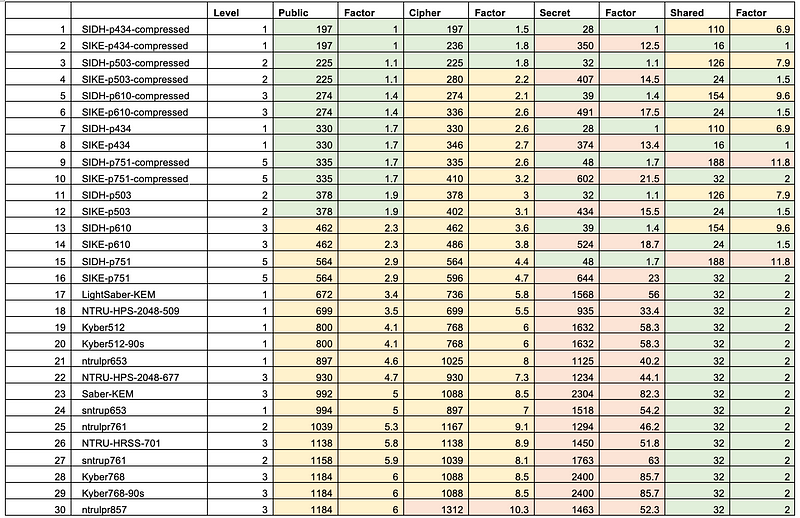
In elliptic curve methods, the public key is only 32 bytes. It also supports perfect forward secrecy (PFS) and which stops the long-term key from being compromised, on the cracking of a single key (neither NTRU [here] Ring-LWS [here] are setup for PFS). Optimised code has shown the key parameters can be generated with 200 milliseconds, and the code has even been ported to ARM processors. The method is still relatively slow compared with elliptic curve methods (and requires around 50 million cycles of a processor). We can see in the following that SIKE-p434 is over 261 times slower than Kyber512 for key generation, 311 times slower for key encapsulation, and over 237 times slower for key decapsulation:


Creating an isogeny
If we have two elliptic curves (E1 and E2), we can create a function that maps a point (P) on E1 to a point Q on E2. This function is known as an isogeny. If we can map this function, every point on E1 can be mapped to E2. Our secret key is then the isogeny, and the public key is the elliptic curve. For key exchange, Bob and Alice mix their isogeny and the other side’s curve to generate a secret curve.

With isogenous elliptic curves we thus do not deal with a single elliptic curve but a family of them [paper]. An isogeny is then a map ϕ: E1 -> E2 and where points on the source curve E1 map to the target curve E2. It turns out that for every isogeny ϕ: E1 -> E2, there’s a dual isogeny ϕ: E2 -> E1, so we can say that two curves are isogenous if they’re linked by an isogeny:

Let’s take an example of Bob and Alice generating the same shared key (as we do with the Diffie-Hellman methods). First Alice has a starting curve of E0, and four points on that curve: PA, QA, PB, QB.
Alice then selects two random values ma and nA and keeps these secret. These will be scalar values.
She then determines a secret point Ra which is:
Ra=ma×Pa+na×Qa
This is her secret isogeny (ϕa). She then transforms Pb and Pq with this isogeny, and where Alice evaluates ϕA at point Pb, and at Qb.
She then sends Ea (her public key), and two transformed points (ϕA(Pb) and ϕA(Qb)) to Bob.
Bob does the same but swaps the a and b values Pa for Pb, Qa for Qb and vice versa. He will generate his own random values mb and nb. Bob calculates his secret: (ϕB).
The following defines the exchange [1]:

Next, Alice uses Ea, ϕa(Pa), ϕb(Qa) to construct an isogeny ϕ′a using ma×ϕa(Pa)+na×ϕb(qa).
Bob uses Ea, ϕa(Pb), ϕa(Qb) to construct an isogeny ϕ′b using mb×ϕa(Pb)+nb×ϕa(Qb).
Now ϕ′a maps to a curve Eab, and ϕ′b maps to Eba, and we can define them is isomorphic. After this, we can calculate a value from the j-invariant, and where j(Eab) is equal to j(Eba), and this will be the same shared secret between Bob and Alice. For a curve of y²=x³+px+q , the j-invariant is:

At the end of this, Bob and Alice will have the same key, and they will know that a quantum computer will not be able to crack it and that no previous keys can be cracked.
The following is an outline of the code [here]:
A sample run is [here]:
SIKE (Supersingular Isogeny Key Encapsulation) for KEM SIKEp503
Public key size: 378
Secret key size: 434
Ciphertext size: 16Public key (only showing 1/8 of key): 64c209b4c7a10a085e4e70506f09103cc39beae3a41603a452b69b59d4e56ef7d04d9508f7d86f4336236a12bb23eb
Secret key (only showing 1/8 of key): 86e22023d7aec17293c6d55d999cdafbf718e59d0b30e60286e22023d7aec17293c6d55d999cdafbf718e59d0b30e602e8b92ccafa7d
Cipher text: a6bb0b631f1743c895015a48cfc33ee882bcbe1a915ccd0c166ce04e4a61602aeb8b1c48386acb364ba22f86337bcf64cd82Key (A): 1f8a0606f64966bfdeaa82d2884e3f2d
Key (B): 1f8a0606f64966bfdeaa82d2884e3f2d
Keys are the same
And here is the running code:
https://asecuritysite.com/pqc/sike
If you prefer Golang, the code is here:
Conclusions
While quantum computers crush RSA and ECC (Elliptic Curve Cryptography), there is still life left in elliptic curves, and isogenies may be their way to continue on into the future. What is definite, is that we need an alternative to lattice methods, and my money is on isogenies to be its main contender. Unfortunately, it’s quite new and needs a bit of time to mature. In crypto land, a decade is perhaps not enough time to properly probe a method. It’s still a little slow in places, but it was can start to optimize it, we will be on a winner.
If you are interested in Post Quantum Cryptography, here are many of the current methods:
References
[1] Costello, C. (2017). An introduction to supersingular isogeny-based cryptography. ECC. [paper]
[2] Jao, D., & De Feo, L. (2011, November). Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In International Workshop on Post-Quantum Cryptography (pp. 19–34). Springer, Berlin, Heidelberg. [paper]
[3] Costello, C., Longa, P., & Naehrig, M. (2016, August). Efficient algorithms for supersingular isogeny Diffie-Hellman. In Annual International Cryptology Conference (pp. 572–601). Springer, Berlin, Heidelberg. [paper]
[4] Douglas Stebila, Introduction to post-quantum cryptography and learning with errors, Summer School on real-world crypto and privacy, Šibenik, Croatia, June 11, 2018 [slides].