A Simple Bet … On Prime Numbers

A Simple Bet … On Prime Numbers

Okay. So, Eve, The Magician has a new TV show with a new trick. She talks to the camera and announces:

“For one night only, I want you to stake $1 on a bet. For this, you will generate a random number, and I will do the same. If those numbers share a factor, I will give you your money back, and will pay you $1 more. Think about it, half of the numbers are even. And you can play this game as many times as you want. It’s a licence for you to print money!”

Bob is watching at home and believes it’s a good bet, as surely he will win, as both Eve and him could pick an even number, and he’d be a winner at least half the time. Then there are all the other numbers that are divisible by 3, 5, and so on. So, Bob goes to his bank and withdraws $100,000, and tries 100,000 times. In the first few attempts, Bob wins more than he loses, and so he continues. But, by the end of the night, Bob has lost $39,200, and Eve — after taking all her winnings from the other players — is a multi-billionaire. But, how could this happen?

Well, it’s obvious that if either Bob and Eve pick a prime number, then Bob will lose the bet. But, we also have co-prime numbers, and where we have two numbers that do not share a common factor. This could be 21 (3x7) and 44 (4x11 = 2x2x11).

Thus, with all the even numbers, Bob thought that he would have at least a 50/50 chance of winning. But, Eve tricked him, as the chance of them both getting even numbers is only 1-in-4.

So let’s compute the chance of Eve winning. For this, we need the help of the gcd() function, and which computes the greatest common denominator between two values. If we get this to be unity (1), the values to do share a common factor. So, we will take a million samples, and for any numbers that are between 0 and the maximum integer number that Python can cope with, we can create the code of:

If we run we get:

For 1000000 pairs, we get 608178 coprimes. This distribution is (60.82%)

And, so, we see it was a bad bet, as around 60.8% of the numbers drawn will be co-prime, and will not share a factor. Thus, Eve will win around 60.8% of the time, so for 100,000 bets, she will win around 60,800 of them.

But, running a long simulation can take time, so is there a better way? Well, we can start off with a 1/4 chance that the numbers are divisible by 2, or:

For it to be not to be divisible by two, it is then:

Then the chance of Eve and Bob picking two values which are divisible by three will be:

and so on. Next, we will try the prime of 5, then 7, then 11, and so on. We thus get the probability that Eve will win is:

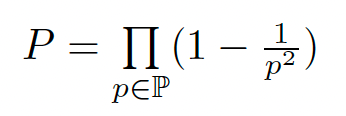
and where p is all the prime numbers. In this case, we have a product of the probabilities to give us the result. Now we can easily compute the chances of Eve winning:

This gives us:

For 1000000 pairs, we get 607704 coprimes. This distribution is (60.77%)
Co-prime rate: 60.80%

And we see that the chances of Eve winning is around 60.8%. Thus there are around 40.2% of values are co-prime. The formula we used above is now similar to the form of the Euler product:

The left-hand side of this formula defines the Riemann zeta function, and this is an important function for the security of public-key encryption. This magical little function allows us to quickly estimate the number of prime numbers we can have in a given range. This is important, as public-key encryption relies on there being enough prime numbers around so that Eve can find the right ones.

Counting primes

Many of our public key methods rely on prime numbers, as they have wonderful properties, including a way of performing mathematical operations on numbers, but constrain them with a finite field (and where our maximum number is the prime number less one). The difficulty in RSA, for example, is to factorize the value of N into the two prime numbers which created N. If these are found, we can easily find out the decryption key associated with the encryption key [here].

The Greek mathematician Euclid showed that there is no “largest” prime number, and we can go onto infinity and never find the last prime.

So, if we pick a prime number of a certain size, how do we know how many prime numbers an intruder has to search through to find the one (or ones) we have used? If we select a small value, such as between 0 and 15 (4 bits), it is not going to be difficult, as the prime numbers will be:

2, 3, 5, 7, 11, 13, 17 and 19

And, if we pick 10⁵⁰, how can we estimate the number of prime numbers there are? Well, in cryptography, we can use the pi(x), function to estimate the number of primes between 0 and x.

One of the simplest methods of calculating π(x) is to generate them and count them. The following code does a sieve derived from a method defined by the Greek mathematician Eratosthenes. With this we filter out multiples of each prime [here]:

One of the methods used is to calculate the prime counting function π(x) is to use the Schoenfeld’s inequality:

One method which can be used to estimate the number of prime numbers is the Riemann R function. This is a smooth approximation for π(x). The function is defined using the rapidly convergent Gram series:

A sample run is [here]:

Range from 0 to  1000000
Estimation of primes:			78498
Possibility of finding prime (%):	7.8498
----- Using Riemannr method to estimate
Estimation is:	78527
Range	Est number of primes
10^ 1 	4
10^ 2 	25
10^ 3 	168
10^ 4 	1226
10^ 5 	9587
10^ 6 	78527
10^ 7 	664667
10^ 8 	5761551
10^ 9 	50847455
10^ 10 	455050683
10^ 11 	4118052494
10^ 12 	37607910542
10^ 13 	346065531065
10^ 14 	3204941731601
10^ 15 	29844570495886
10^ 16 	279238341360977
10^ 17 	2623557157055978
10^ 18 	24739954284239496
10^ 19 	234057667300228928
10^ 20 	2220819602556027136
10^ 21 	21127269485932298240
10^ 22 	201467286689188773888
10^ 23 	1925320391607837261824
10^ 24 	18435599767347541311488
10^ 25 	176846309399141946490880
10^ 26 	1699246750872419937812480
10^ 27 	16352460426841662628560896
10^ 28 	157589269275973244548022272
10^ 29 	1520698109714271704874745856
10^ 30 	14692398897720432138328735744

In this case, if we were to select a number at random between 0 and 1,000,000, the probability that we will find a prime number is 7.84%. Often when we pick a random prime number, we start with a random number, and then keep subtracting one from the value, and testing it, until we find a prime.

And so, if our attacker can try 1 billion prime numbers per second, then if we select a prime number in the range of 10¹⁵, it will take around 29,800 seconds — or just eight hours — to try them all. So we need to make sure that the prime number size is large enough so that an intruder will have too many prime numbers to find in order to crack the keys.

If you are interested 10³⁰ is equivalent to 99 bits. Normally, with RSA, we use 2,048, so there are lots of primes that an intruder would have to search through. Here is my little simple Python code that converts 10³⁰ to bits:

>>> import math
>>> y=10**30
>>> print math.log10(y)/math.log10(2)
99.6578428466

We can also estimate the number of prime numbers for a given bit size [here]. If we run for 512 bits, we get:

Estimate the number of primes for a given prime number size.

Number of bits in prime number: 512
Estimated number of prime numbers is: 18906370642694533330255267422559435438516148269380861172414282021437571915512683767157742768034244490543655250659082340701872652735175220791902826659840
Chances of finding a prime:  0.28 %

And so for a 512-bit number, we have 0.28% chance of finding a prime number. The number of prime numbers is estimated at 18906370642694533330255267422559435438516148269380861172414282021437571915512683767157742768034244490543655250659082340701872652735175220791902826659840, and so searching for a given prime number for every 1 nanosecond will take: 5.99 (and 134 zeros) years — that’s a long time.

Conclusions

As is always the case, Eve tricks Bob. And, so, I leave you with [here]: