CTF Generator: Low private exponent (d) in RSA … the Wiener attack

CTF Generator: Low private exponent (d) in RSA … the Wiener attack

I am working on a set of automated Cipher CTF (Capture The Flag) challenges, and part of this is to create methods which aim to break RSA. If you are interested, here are the RSA -related ones I’ve already completed:

• CTF Generator: Cracking RSA with Chinese Remainder Theory — Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
• CTF: RSA Challenge Generator. RSA. This provides values for e and N, and gives the cipher, and you must crack it by finding d.
• CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA.

So, this morning, I implemented the Wiener attack [1] on RSA keys which have a relatively low private exponent (d):

In RSA, we select two prime numbers of equal length (p and q), and then multiply these to give a modulus:

We then compute the ciphertext as:

and where we decrypt with:

With this, we have a public exponent of e, and a private exponent of d. The value of d is computed from:

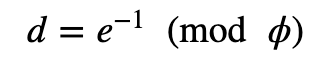
and where:

While these days, we normally use e=65537, we could select a range of values of e. If we select a fairly large value, then the value of d could be discovered. In this case, we will use the Wiener attack [1] to discover p, q and d.

For this, we have a public key of ⟨e,N⟩, N=pq and q<p<2q . So if:

then d can be recovered by searching k/d among the convergents of e/N. The following code is based on [here]:

from Crypto.Util.number import long_to_bytes,bytes_to_long
from Crypto import Random
import Crypto
import sys
import libnum
from math import isqrt

from sympy import *
import random

def get_prime(bits):
	p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
	return(p)

# Rational numbers have finite a continued fraction expansion.
def get_cf_expansion(n, d):
    e = []
    q = n // d
    r = n % d

    e.append(q)

    while r != 0:
        n, d = d, r
        q = n // d
        r = n % d
        e.append(q)

    return e

def get_convergents(e):
    n = [] # Nominators
    d = [] # Denominators

    for i in range(len(e)):
        if i == 0:
            ni = e[i]
            di = 1
        elif i == 1:
            ni = e[i]*e[i-1] + 1
            di = e[i]
        else: # i > 1
            ni = e[i]*n[i-1] + n[i-2]
            di = e[i]*d[i-1] + d[i-2]

        n.append(ni)
        d.append(di)
        yield (ni, di)

def create_keypair(size):
    while True:
        p = get_prime(size // 2)
        q = get_prime(size // 2)
        if q < p < 2*q:
            break

    N = p * q
    phi_N = (p - 1) * (q - 1)

    # Recall that: d < (N^(0.25))/3

    max_d = isqrt(isqrt(N))// 3

    max_d_bits = max_d.bit_length() - 1

    while True:
        d = random.randint(0,2**max_d_bits)
        try:
            e = pow(d,-1,phi_N)
        except:
            continue
        if (e * d) % phi_N == 1:
            break

    return  N, e, d, p, q

msg="Hello"
bits=128
if (len(sys.argv)>1):
        msg=str(sys.argv[1])
if (len(sys.argv)>2):
        bits=int(sys.argv[2])

m=  bytes_to_long(msg.encode())

N, e, d, p, q = create_keypair(bits)

C=pow(m,e,N)

print(f'Bob uses RSA to send an encrypted message to Alice. The public exponent (e) is {e} and the modulus (N) is {N}. With a cipher of {C}, determine the decrypted message:')

cf_expansion = get_cf_expansion(e, N)
convergents = get_convergents(cf_expansion)

for pk, pd in convergents: # pk - possible k, pd - possible d
	if pk == 0:
		continue;

	possible_phi = (e*pd - 1)//pk

	p = Symbol('p', integer=True)
	roots = solve(p**2 + (possible_phi - N - 1)*p + N, p)

	if len(roots) == 2:
		pp, pq = roots # pp - possible p, pq - possible q
		if pp*pq == N:
			print('\nAnswer:')
			print('Using Wiener attack')
			print('Found d:',d)
			print('Found p:',pp)
			print('Found q:',pq)
			print('Found PHI:',possible_phi)
			print('Now using C^d mod N')
			M=pow(C,d,N)
			print(f"\nDecipher: {long_to_bytes(M)}")
			sys.exit(0)

print('[-] Wiener\'s Attack failed; Could not factor N')
sys.exit(1)

A sample run for a modulus of 256 bits is:

Bob uses RSA to send an encrypted message to Alice. The public exponent (e) is 43871681663324392533127781481009362400584674864304806646491757416665595523303 and the modulus (N) is 44466357534339575017860083247573877407618031516680311133883139663695835208893. With a cipher of 43902765653352906059943880269521181498770230735446008058649859731568013764582, determine the decrypted message:

Answer:
Using Wiener attack
Found d: 4194341459785600727
Found p: 197877740962711720186826779166020766833
Found q: 224716318864378282922995753259834583821
Found PHI: 44466357534339575017860083247573877407195437456853221130773317131269979858240
Now using C^d mod N

Decipher: b'abc'

So, if you are an eager student (and we are all students of some form), or want to generate challenges for your students, here is the challenge generator:

https://asecuritysite.com/rsa/rsa_ctf04

and here is the solver:

https://asecuritysite.com/rsa/rsa_ctf05

So here’s a challenge for you:

Bob uses RSA to send an encrypted message to Alice. The public exponent (e) is 72346057606464611965416673142428864369242668619028107101120465554803081436731 and the modulus (N) is 78821919615049121282446060740822935483766681740557816303517540176403696360971. With a cipher of 45915720098628515386324213246149352612336524174187945728330971084073293182313, determine the decrypted message.

The answer is a UK city.

Conclusions

We are pretty much fixed on e=65537, so d is highly unlikely to be small (if we use a large enough modulus). But, it’s an interesting method and allows you to get into cryptanalysis. Go learn some RSA crypto … [here]:

References

[1] Wiener, M. J. (1990). Cryptanalysis of short RSA secret exponents. IEEE Transactions on Information theory, 36(3), 553–558. [here].