Damgård-Jurik Homomorphic Encryption With Secret Shares

Damgård-Jurik Homomorphic Encryption With Secret Shares

Well, what a day … Boris Johnson has stepped down as the PM in the UK. For some in the UK, it is a happy moment.

And so, there will be a ballot to elect a new PM. But, just imagine if we could build an election system which truly preserved the privacy of voters, and which distributed the computation of the result over a distributed network? We could then generate cryptographic proofs that everything was working correctly, and that every vote was counted, and in a correct way. It would then integrate encryption, privacy-preserving methods, proofs of knowledge and resilience — and be an election which was fit for the 21st Century.

I appreciate that for the election of Boris’ successor, that this will not happen, but maybe in the future we could see these methods applied into general elections.

Homomorphic Encryption and Secret Shares

Over the next decade, two major areas of developments within cybersecurity will be the usage of homomorphic encryption, and Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels, especially if we can combine the two of them.

So let’s look at the Damgård-Jurik method [here]:

In this case, the method uses Paillier encryption, and where there is a single public key and a private key which is split into shares (using Shamir’s secret sharing method). This public key then encrypts values, and which can then be operated with arithmetic operation, and then decrypt the result with the private key. This private key can only be reconstructed by the trust of the key share holders.

Paillier Encryption

With Paillier encryption, we select two large prime numbers (p and q) and compute:

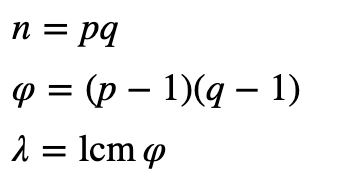
and where lcm is the least common multiple. We then select a random integer g. We must make sure that n divides the order of g by checking the following:

and where L is defined as:

The public key is (n,g) and the private key is (λ, μ). To encrypt a message (M), we select a random r value and compute the ciphertext of:

and then to decrypt:

For the public key we might have:

n=2161152757, s_p=540264619

and where p =39,323 and q=54,959. We also compute the product of Sophie Germain primes: s_p= p_prime * q_prime where p = 2 * p_prime + 1 and q = 2 * q_prime + 1. A demo of Paillier key generation is here:

https://asecuritysite.com/homomorphic/palkeygen

Coding

Now let’s code the Damgård-Jurik method [here]:

and a sample run [here]:

Using Damgard-Jurik method with 64-bit key, and a threshold of three and three shares

Public key. n=174743826971117924232203186477859825289, s=1, m=43685956742779481051423225748488060689, threshold=3, delta=6

val_1: 9
val_2: 3

c_1: 27429320619805987848765352451564237217145248338366944942206061954884249278992
c_2: 14769913771126168413630660895236067257037103416139804498830583273184880216135
c_1+c_2: 12086035254029813325315665006256800980915988130367594983597188460984693331181
c_1-c_2: 921687804424968958981627966721274246800285129994018401822135562246021703624
c_1*c_2: 21809874053261031282086634289802837387921962314468453992976726818561314427636

Decrypt (Add): 12
Decrypt (Subtract): 6
Decrypt (Multiply): 27

I have created a demonstrator here:

https://asecuritysite.com/homomorphic/damgard

And there’s an online simulator here:

http://security.hsr.ch/msevote/damgardjurik

p = 7, q = 11, n = pq = 77, φ(n) = 4n' = 60, λ(n) = lcm(p-1,q-1) = 2n' = 30

p'= (p-1)/2 = 3, q'= (q-1)/2 = 5, n'= p'q'= 15

s = 2, ns = n^s = 5929, n^(s+1) = 456533

Valid Voting Messages:        m = mi, None: m0 = 0, C1: m1 = 1, C2: m2 = b = 6, C3: m3 = b^2 = 36

Damgård-Jurik Private Key:    d = x*λ(n) = 2174*30 = y*n^s + 1 = 11*5929 + 1 = 65220

Damgård-Jurik Encryption:     c[m,r] = g^m * r^(n^s) mod n^(s+1), with generator g = (n+1)^α * &beta^(n^s) mod n^(s+1) = 20704  (α = 41, β = 61)

The paper defines a way of splitting the private key, and which allows decryption to be split over a number of secret shares for the computation of a final result in an election. For example, we might split the share in 1,000 elements, and where the private key is split over a range of hosts — each which can compute one part of the final result. With the Shamir method we define a threshold value (t) for a number of shares (n). We would thus need at least t hosts to come together to agree to regenerate the result of the election. This would guard against one or more of the nodes becoming bad, and be taken over for malicious purposes — we then have Byzantine Fault Tolerance (BFT).

And there’s an online simulator here:

An example is:

p = 7, q = 11
n = pq = 77
φ(n) = 60
λ(n) = lcm(p-1,q-1) = 30

p'= (p-1)/2 = 3, q'= (q-1)/2 = 5, 
n'= p'q'= 15

s = 1
ns = n^s = 77
n^(s+1) = 5929

Valid Voting Messages:        
m = mi, None: m0 = 0, C1: m1 = 1, C2: m2 = b = 6, C3: m3 = b^2 = 36

Damgård-Jurik Private Key:    
d = x*λ(n) = 18*30 = y*n^s + 1 = 7*77 + 1 = 540

Damgård-Jurik Encryption:     
c[m,r] = g^m * r^(n^s) mod n^(s+1), with generator g = (n+1)^α * &beta^(n^s) mod n^(s+1) = 5288  (α = 41, β = 61)

Conclusions

While elections are unlikely to move to these trusted methods any time soon, there are so many things we can apply this method too, especially within third party processing of data.

If you want to learn more about homomorphic encryption, try here:

https://asecuritysite.com/homomorphic/

and for secret shares:

https://asecuritysite.com/shares/

Conclusions

We have trusted methods of computation at our fingertips, but we are often held back by a lack of trust in these methods, both from a human and digital point-of-view. Hopefully, though, things will change, and we will start to see an increase in the proper integration of cryptographic trust within our computing infastructures.

References

[1] Damgård, I., Jurik, M., & Nielsen, J. B. (2010). A generalization of Paillier’s public-key system with applications to electronic voting. International Journal of Information Security, 9(6), 371–385.