Fun Facts With Encryption Keys: What Takes 183,587 Million Million Million Million Million Million…

Fun Facts With Encryption Keys: What Takes 183,587 Million Million Million Million Million Million Million Million Million Years to Crack?
I once heard from a company that was advised that they should migrate from 128-bit AES to 256-bit. The advisor said that 128 bits could be easily cracked. As will we find, it is certainly possible to crack it, but it will take 539 million million million years to do so (on average) for a fast encryption cracker.
The basics of keys
With symmetric key encryption (such as with AES encryption), an encryption key is used to encrypt plaintext into ciphertext, and decrypt ciphertext to plaintext. The more keys we have, the longer it will take, on average, to find the correct key. For example, if we have a 4-bit value, we will have 2⁴ keys (16).
Overall, the number of encryption keys will be 2^n. If we try M keys per second, then the average time to crack by brute force will be 2^n/(2.M) seconds. If we have a 36-bit key, we then have 3,668,719,476,736 (2³⁶ keys), and if we can try 10 billion keys (10x10⁹) keys per second, it will take 3.44 seconds on average to find the correct key. Here is a simple calculator for the times to crack various sizes of keys using 10 billion keys tried per second:
https://asecuritysite.com/principles/key?keys=10000000000
Now let’s try 128-bit and 256-bit randomly generated keys
Normally, for AES encryption, we use either 128-bit or 256-bit keys. So, let’s see how long it would take to crack them by brute force, and for a randomly generated encryption key.
For a 128-bit key, we have 340,282,366,920, 938,463,463,374, 607,431,768,211,456 different keys (2¹²⁸). If we now crack at 10 billion keys per second, the average time to crack will be 539,514,153,540,301,000,000 years. That is 539 million million million years!
Now, let’s try a 256-bit key.
For a 256-bit encryption key, it would take 183,587,153,154,040,000,000, 000,000,000,000,000,000,000,000,000, 000,000,000,000 (183,587 million million million million million million million million million) years to crack using brute force, and with 100 billion keys tested per second.
But, what about increasing computing power?
But … I have been tricking you, as this computation just bases the time on current computing performance. If we double our computing power every year, it will take half as long in the next year, so on. When Ron Rivest outlined the RSA method in 1979, he based his computation on two 63-digital prime numbers that would be multiplied to create a 126-digit value:
Contrast this with the difficulty of finding the two prime factors of a 125- or 126-digit number obtained by multiplying two 63-digit primes. If the best algorithm known and the fastest of today’s computers were used, Rivest estimates that the running time required would be about 40 quadrillion years’
A 256-bit number, at its maximum, generates 78-digits [here]:
115,792,089,237,316,195,423,570,985,008,687,907,853,269,984,665, 640,564,039,457,584,007,913,129,639,936
The 40 quadrillion years has not quite happened, and where 512-bit keys are easily broken in Cloud. If you are interested, here is a 512-bit integer value and which has 148 digits, such as [example]:
13,407,807,929,942,597,099,574,024,998,205,846,127,479,365,820,5 92,393,377,723,561,443,721,764,030,073,546,976,801,874,298,166,9 03,427,690,031,858,186,486,050,853,753,882,811,946,569,946,433,6 49,006,084,096
The search for prime numbers, too, has been progressive since 1977, and by 2014, the world discovered a 17,425,170-digit prime number. The finding of prime numbers makes the finding of them in the RSA method must easier.
Overall, we lose about one bit of security strength every 18 months (if we advance assuming Moore’s Law).
But, what is the cost?
But, time is just a function of the number of processors that we can use to crack the keys. The more cores we have for our GPUs, the faster it will take to take the encryption key. In order to properly understand the concept of work in cracking cryptography, Lenstra [here] defined the concept of Global Security in order to show the amount of energy required to crack cryptographic algorithms. He then compared this with the amount of water that energy could boil something. But, overall, energy costs money, and so we get an overall cracking cost in terms of $, ¢ or £.
This could be seen as the carbon footprint of cracking. For a 35-bit key symmetric key (such as AES), you only need to pay for the boiling of a teaspoon of energy, and for a 50-bit key, you just need to have enough money to pay for a shower:
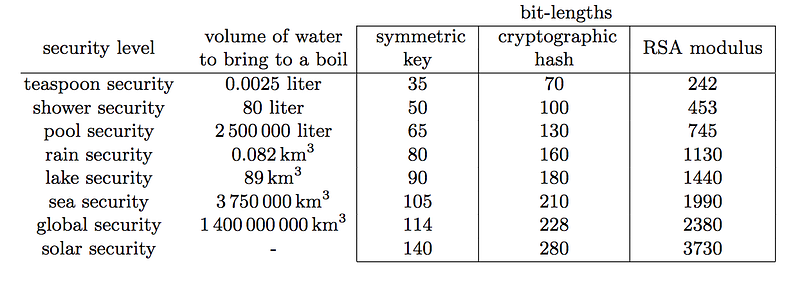
For our 128-bit key, we would need to boil all the oceans on the planet — many times over … just to crack a single key.
So let’s look at asymmetric encryption, such as for RSA. In order to crack it, we need to factor N, into p and q (the two prime numbers used). Once cracked we can determine PHI (p-1 x q-1), and then we can determine the decryption value (d) [here]. First, we will take teaspoon security, and where we would need to consume the amount of energy that can boil a teaspoon. A sample would be (242-bit RSA modulus) [here]:
N=p*q= 5896261486983538627098661478596873684661596787145726508859641645687965941
The prime numbers have 121 bits, and, if we were to crack it, the prime numbers are:
(p): 2526944374765758521282783272842906989
(q): 2333356264531983395509730755656883369
Now we try swimming pool security, which will have a 745-bit modulus [here]:
N=p*q= 32820593417068637302218774761235133563284012029917056683084157063791880518253729060356882948911691226183490705953686023149594165668325095998315760949745673726122108730625118573143944403355956100353972339795087626332085413773
You would then have to consume the amount of energy to boil a swimming pool of water, in order to recover p and q, and which would be:
(p): 5136574890107321107930054184342872847511932740355863615831749987190796683508207354267329960601590388187075433061
(q): 6389587248163902409204449208538775019640799414724150251382810569000364623759594714615114512184726059299258653193
Now, for a 2K modulus, we would have to get the energy to boil all the seas in the world in order to factorize this [here]:
N=p*q= 43167595701317556262423026656965675311752941263790242843723869722559144737611460632568632166086252510023021805945735591772225470974213720757550705733352824448503063524999506226660596906575816882736759369162417329042308450768818539569647978275834799861395280256322795630706924323442073941650079693323544638961692274755658766444829616155400362106306476222028695948219411648554898625217423276610753800859051583718732195244823763757178756946886496848799638990325775625765337088319529344897632569507945680260646306289624365294219736449252864209416787913390862597496737460530614841627093463597005887159713
If you could afford the energy to boil all the seas on the planet, you would be able to recover the prime number factors of:
(p): 196609148217569855881469103057436778288884865730728431036496969106242709174542556226244974424242605165013577403243273721574500460326174617160923703395095978667090714867455310166651932606597318485468745721964757615177804666962624050069365974032392172635080905056653578728556376998092239415714121906067
(q): 219560463450804526512484156665207894511493329487508026519690092833541901773486924130405885017845670513121751269792879364231218578683707161192474640518621978728363979172391042793592947789410287416485864619629721775927035570271970144478351754084252110756000450203907965120369883036301470716442779209339
Finally we move to solar security (4K modulus) [here]:
N=p*q= 3960081571383420167814679941098524090937928309488590816012966209196161594447717629829982817426147699500858353736336886688538212500739476494518433176312774088968991333976947698248519629991492642529120005788698131019622899051239531916630515702854026672543263467130654985378038454931630236636653155999253153667000741616739898252666802505968932136484029166497432922043251656271894573751299513374223876341473788971768959659494093660332016468558662263427959769631314190762350433414241237989194424754061077772372503406770663167105510157438848063647609081050040392193568744736442564106876056012592222564834186803873526496760807948668990042316968129375782077793420316049776474546085038021971914974545368413754514832542993932007256348508892381012868762395242004260990250419466271752664052646884549601175933263521857652478403283808673329360714989274196579539004889158891187902257130712437178153193341806763422097034483621244566078923257429637598615691552350410659591140346748167709449018947885391433407732878878772283602778821869413553383175098670195132506173740601661352893351053048344129586887687118260226198269183634491741066922963
You will never find the prime numbers, but they are:
(p): 2387628035654914041578676682340635535950948791037039903330270590495501744849764207480076462162294270197243407459110192208709737698247332428053357258855955290692393471421516310661792749482905080962109692416944336517049095407867686284521225687878370847230533829287501911033500368831913293493330562838467387835530549969054109399131451846959457130413492668037089837378118350872377084885693225874836148717207853352068189405415387476462556003921350678166912349980061364631958090280213640154021116006326720158290040518790513066623093136091263566334119222952846436577451
(q): 1658583963769377603578396329705793644732710623310129654038348230711585763044092787355651332948374169988931521882298144371384733551640579147022118494636732293264604461116977329421823894181755805820089237394172033870263627093736577790369697957516336302977958796425947479274422794199973433467842572527064416348509712003954901454840352976743534063167992440103943082723957859216188269111695713462656653049479588103312185114742167076660911677070759504987871743971457634287384430572107927280368523691106585718147625665698291217102305172813935222056309427697965967221113
But, what about quantum computers?
Well, quantum computers will speed up symmetric key and hash cracking, but we still have a massive margin in terms of the time to crack. Perhaps, we will jump to 256-bit keys, soon? But, for asymmetric encryption (public key encryption), the game is over. These methods are based on techniques that can be easily solved by quantum computers, so RSA, ECC and discrete log methods will be almost cracked instantly (such as using Shor’s algorithm).
One of the strangest papers you’ll read about RSA is from the famous Daniel J Bernstein [here]:

Daniel is famous for inventing the Salsa stream encryption method [here], and proposed Curve 25519 elliptic curve [here]. In the 1990s he fought against US export controls for cryptography in the design of secure email and DNS services, and, in 1995, he ended up suing the US Government. Bernstein’s objective is to “Make RSA Great Again!”, and sets about testing the limits of Shor’s algorithm for RSA, and pushes it further so that a quantum computer could not crack it within a reasonable cost.
The PQRSA paper is rather weird, but maybe I just don’t get the objective of it. In it the authors focus on extending the RSA method by using an exponent of just 3 (e=3), and also using an N value which is made up for many prime numbers. The resulting key size is … wait for it … 1 Terabyte. Yes. One Terabyte. Just now I type this article on a Macbook Pro, and which has a total storage of 1TB! Are we being serious? In order to overcome quantum methods, we need to create a key which would struggle to fit on most laptops.
The 1 TB key with an exponent of 3 requires ²³¹ (2,147,483,648) 4,096 bit primes (they are extremely large by today’s standards), and which takes around 1,975,000 core-hours to compute (which is four months to generate on a 1,400 core cluster). On my Mac I have four cores, so it would take over 20,000 days to generate a key. And then you are left scratching your head when you read that for 256GB encryption, the total time to encrypt was over 100 hours (362015 seconds) — see the table below. For decryption, a 32 GB file took over 17 hours. The N value is thus created from multiple prime numbers, and the Chinese Remainder Theorem (CRT) is then used for encryption and decryption. Their method also used 3.166TB of RAM and 2.5 TB of swap storage — on my Macbook I have 16 GB of RAM, so they will have to give computers a whole lot more memory if they were to use a quantum robust RSA method.

Conclusions
Now, even the NSA does have the money to boil every ocean on the planet — just to crack a single encryption key. But, while it will take 539 million million million years, on average, to crack a randomly generated encryption key, it will take less than a second if you give away the password that protects it. So, don’t click on that dodgy link!
Here’s my basic table of key sizes and times to crack …