John Napier Legacy Lives on With Privacy and Cybersecurity: Meet NI-ZKPs with Discrete Logs

John Napier’s Legacy Lives on Within Privacy and Cybersecurity: Meet NI-ZKPs with Discrete Logs
I am privileged to walk past John Napier almost every time I go to work. Well, I walk through John Napier’s Tower, but I think about his legacy in this modern world each time I walk through it. With this, we see discrete logs used in the Diffie-Hellman method and in Zero Knowledge Proofs (ZKPs). While we have mainly replaced discrete log methods with elliptic curves, we still retain the formal proofs within discrete logs.
Some basics
Before we start, let’s do some simple logarithm rules. Two basic rules that were defined by John Napier are:

In discrete logarithms, with then perform a (mod p) operation and where p is a prime number. And so we have:

Discrete Log Proof of Equality (DLEQ) with discrete logs
We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the ‘Prover’) just has to prove that she still knows her secret. In an interactive version, Victor (the ‘Verifier’) sends Peggy a challenge, and Peggy can prove that she can provide a solution for it. In a non-interactive version, Peggy can create her own challenge.
Initially, Peggy creates a secret value (x) and has two bases of g and h. She then creates two values g^x and h^x, and can check that:

Peggy creates:

The value of x cannot be discovered from xG or xH. For the non-interactive proof, Peggy generates a random value (v) and computes:
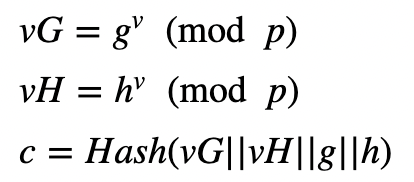
and then:

The proof is then (xG, xH, r, c). The values of g, h and p will also be public. Victor will prove this by computing:

If c==c_1, the proof is valid. This works because:

In the following, we will use SHA-256 for the hash, and convert each of the values into byte arrays. For example, we can convert vG into a byte array of bitsize/8 bytes with vG.to_bytes(bitsize//8,”big”), and where we have a big endian arrangement. If we have 256-bit prime numbers, then we will need 32 bytes to store our values. The “||” operation is byte concatenation, and which is just implemented with a “+” in Python [here]:
A sample run for 64-bit primes is[here]:
== DLEQ ===
Secret: 8226441489057554051
p: 14312102784525063139
g 1432205245299627649
h 1058739418500529656
g^x 7369471065254115060
h^x 6372925570753712066
r 4550682446127323237
c 5831082032206369735
Proven True
Now trying with incorrect proof
Proven False
and for 512-bit primes is [here]:
== DLEQ ===
Secret: 4485923188924488412770095380084849302359769199219096921170805950233341673039507161998488923082887225958486548919069894042865192224684466800184387418144578
p: 10230815590986016812047309420680505393360441133418520160704811548022578456158580345721760786630989892998747886706490392737716774229655732916369444120480187
g 7929877076908562502316486448368602866215898966493039131680085215597578644481201738567710044283149594248296095486527916650843450010811632410794845598912745
h 1381406091123889617542991225438794380465883840037416312798346438002064792574539898627890768749394931716046279784580490628368171280639918054321448689664433
g^x 2973733723359334947565285084278690365837720254903897779894080144528129155486503303461212284682135822682572314528337823319340443631638156598275813982940222
h^x 1890122968958225767129143110782554241532636340757736170130650192038155592188639366093084038642150642798077442715613551026445162669168485502155742328468755
r 2635232827407747635198519416549648131317415797442254037983046372285289997593843768207483238960999153029489818189173613905695172543688810022597278409695679
c 51564139126147450624294160277058132351029000945450970191196652769905165621350
Proven True
Now trying with incorrect proof
Proven False
And there you go … a way to keep a secret using John Napier’s logs.
If you want to see how it is achieved in ECC, try here:
https://asecuritysite.com/zero/dleq2
Conclusions
We need to stop storing and transmitting private information, and where we can prove our secrets, without giving them away. A non-interactive Zero Knowledge Proof is one way to prove your identity, your biometrics and your password, without ever giving away your secret information. I have outlined a number of ZKPs here: