Hellman, Pedersen and Chaum: ZKPs with the Decisional Diffie–Hellman (DDH) assumption

Hellman, Pedersen and Chaum: ZKPs with the Decisional Diffie–Hellman (DDH) assumption

One of my highlights of the academic year is when two of the greats of computer science came to talk to our students. These were Marty Hellman (the ‘Hellman’ in the Diffie-Hellman key exchange method [3]) and Torben P Pedersen (the ‘Pedersen’ in the Pedersen Commitment [2]) [interview]. Torben remembers keenly working with the mighty David Chaum, so let’s look at a method that combines the DH method with the Chaum-Pedersen method [3] to implement a Zero Knowledge Proof (ZKP).

The Diffie-Hellman part

A typical thing we must prove is that we still hold a secret (private) key. So, how can we bind Victor and Peggy into a proof infrastructure that Peggy can prove to Victor that she still holds a private key? For this, we will bind Victor and Peggy through a Diffie-Hellman key exchange.

Within Decisional Diffie–Hellman (DDH) we have a tuple of ⟨g,g^a,g^b,g^{ab}⟩ and where a and b are secrets. The values of g^a and g^b are exchanged between two parties, and after this, they should both be able to generate g^{ab}:

The Chaum-Pedersen part

If we have Peggy as a prover and Victor as a verifier, then Peggy needs to show that she knows a secret value a. With the Chaum-Pedersen ZKP, Victor generates a commitment for Peggy to produce a ZKP to protect a secret. For this, she will send Victor the value of g^a (mod p). When Victor needs to prove that she still knows a value, he will send a challenge value (s). Alice then generates a random value (r) and sends back y_1=g^r and y_2=B^r. Victor then checks the equality of gz=A^s y_1 (mod p) and B^z=C^s y_2 (mod p). An outline is:

After Victor and Peggy exchange their secrets, Victor will hold g^a (mod p) and Peggy will hold g^b(mod p). For the zero-knowledge proof we thus start with:

Peggy has a secret value of a and generates A=g^a. Victor has a secret value of b and generates B=g^b. They exchange A and B and then use the Diffie Hellman method to generate C.

Victor sends a commitment (s) to Peggy:

Peggy computes a random value (r):

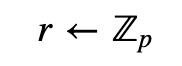
And she sends Victor:

and:

Peggy also sends:

Victor then checks:

and:

If these are true, Peggy has proven she knows the secret (a). This works because:

The Code

The coding is [here]:

import random
import libnum
import sys

bitsize=128
if (len(sys.argv)>1):
    bitsize=int(sys.argv[1])
      
p=libnum.generate_prime(bitsize)
s=random.getrandbits(bitsize)
g=2
a=random.getrandbits(bitsize)
b=random.getrandbits(bitsize)
c=random.getrandbits(bitsize)

r=random.getrandbits(bitsize)
A=pow(g,a,p)
B=pow(g,b,p)
C=pow(g,a*b,p)

y1=pow(g,r,p)
y2=pow(B,r,p)

z=(r+a*s) % (p-1)


print("== Chaum-Pederson ZKP with DDH ==")
print("p=",p)
print("a=",a)
print("A=g^a (mod p)=",A)
print("b=",b)
print("B=g^a (mod p)=",B)
print("ab=",a*b)
print("C=g^{ab} (mod p)=",C)


print("\nProof: g^z = A^s y1")
val1= pow(g,z,p)
val2=(pow(A,s,p)*y1) % p
print("Val1=",val1)
print("Val2=",val2)

if (val1==val2):
    print("- Proof verified")
    
print("\nProof: B^z = C^s y2")
val3= pow(B,z,p)
val4=(pow(C,s,p)*y2) % p

print("Val3=",val3)
print("Val4=",val4)

if (val3==val4):
    print("- Proof verified")

A sample run for 256 bit primes is [here]:

== Chaum-Pederson ZKP ==
p= 71808837207067558396943502247178805470599306337269585872075038503116361400603
a= 36623398984913964172485596625205226031763309121917034188846578869320021978402
A=g^a= 32096207796582799691444233880948982714496908564580085529419678203181985482397
b= 31626404664308059618102781249870451013488637545242770934698960204990436278054
B=g^a= 22868249499514124460303251323889043821880224466294750444534923941031732565838
ab= 1158266436479298052448345755868228483694002563526288816181771624565721107667448582344993414115064433575649547672009235534272667805336831732117954454589708
C=g^{ab}= 8021151953795073005899136029637476282156155200732630284950825682466003109726

Proof: g^z = A^s y1
Val1= 9590670516289397297344719778854690756344241363231213529959870845950311348445
Val2= 9590670516289397297344719778854690756344241363231213529959870845950311348445
- Proof verified

Proof: B^z = C^s y2
Val3= 56336209634019548929170814618015392124101293159018455662661735618180853220223
Val4= 56336209634019548929170814618015392124101293159018455662661735618180853220223
- Proof verified

Conclusion

The only direction for cybersecurity is toward a zero-trust model. One way of stopping data breaches of sensitive information is not to store those secrets, but to replace them with random oracles. If these oracles are revealed, it will reveal nothing of the actual secret. In the method I have outlined, we can easily convert it into a NI-ZKP (Non-interactive ZKP) by hashing the generated values that are using the proof.

If you are interested, here’s Marty talking to our students:

and Torben:

References

[1] Pedersen, T. P. (1991, August). Non-interactive and information-theoretic secure verifiable secret sharing. In Annual international cryptology conference (pp. 129–140). Springer, Berlin, Heidelberg.

[2] Chaum, D., & Pedersen, T. P. (1992, August). Wallet databases with observers. In Annual international cryptology conference (pp. 89–105). Springer, Berlin, Heidelberg.

[3] Diffie, W., & Hellman, M. E. (1976). New directions in cryptography. In IEEE Transactions on Information Theory, Volume: 22, Issue: 6, November 1976.