The Castryck-Decru Attack on SIDH

The Castryck-Decru Attack on SIDH

Bugs, Weaknesses and Tweaks Are A Normal Healthy Part of Cryptography Research

The thing I love about being involved in cryptography is that there is a vibrant and healthy research community. It is one that reads and enacts the latest work from research papers. In order to be up-to-date on the latest methods, attacks and vulnerabilities, you need to keep reading research papers. We see, too, a general strive to improve methods. When a bug is found, there’s often a tweak or a rethink of the methodology.

And, so, from one of the most advanced nations for cryptography research (Belgium), we now have a preliminary paper of [here][3]:

The paper cracks the Level 1 security (equivalent to 128-bit symmetric key security) of the SIDH (Supersinglar Isogeny Diffie-Hellman) key exchange method. One of the main problems here is that the SIDH (Supersinglar Isogeny Diffie-Hellman) key exchange method is proposed as one of the possible alternative methods to post-quantum key exchange. While CRYSTALS-Kyber was a clear winner in the NIST PQC (Post Quantum Cryptography) competition, SIDH is advancing towards standardization as an alternative method. One of its core attributes is that it is not lattice-based, as there is a general worry that a weakness in the lattice methods could be discovered.

So, is SIDH and, more generally, isogenies dead in the water? Well, let’s see.

How do elliptic curves work in public key crypto?

First, let’s talk about elliptic curves. These have the form of:

y² = x³ + ax +b

and where a and b are characteristics of the curve. With this, we might have an elliptic curve of:

y² = x³ + x

In public key cryptography, we constrain this within a finite field using a prime number (p). Our equation then becomes:

y² = x³ + x (mod p)

and where we will only get values for x and y within 0 and p-1. If we select x=1, and p=97, we get our first point at y=83:

83² = 1 + 1 (mod 97)

This because 83² (mod 97) = 2. There is then no solution if we try x=2, x=3, and x=4. The next point is at x=5:

79² =5³+ 5 (mod 97) = 130 (mod 97) = 33 (mod 97)

As 79² (mod 97) = 33.

What’s an isogeny?

An isogeny (“equal origin”) provides a mapping from one elliptic curve to another. In this way, we transform from one curve into another. For example, y²=x³+x maps to y²=x³−4x with the mapping:

The code is [here]:

A sample run [here]:

Finite field: 97

y^2 = x^3 + x (mod 97)		y^2 = x^3 - 4x (mod 97)
(1 83)				    (2 0)	Check (2 0)
(5 79)				    (44 91)	Check (44 6)
(8 61)				    (93 7)	Check (93 7)
(11 88)				    (64 52)	Check (64 52)
(12 73)				    (4 57)	Check (4 57)
(19 66)				    (65 7)	Check (65 90)
(20 39)				    (54 37)	Check (54 60)
(22 0)				    (0 0)	Check (0 0)
(23 68)				    (61 57)	Check (61 40)
(25 79)				    (91 83)	Check (91 14)
(30 89)				    (85 39)	Check (85 39)

The check is correct in this case, as (44,91) is the same as (44,6) as we are using (mod 97). This is because we generate two points for every x value (y and -y).

So what is SIDH

With SIDH — based on SIKE — we use isogenies to create a shared secret key between Bob and Alice. Basically, Bob and Alice start off with the same curve (E0), and then they randomly walk away from the curves. This creates EA (Alice’s curve) and EB (Bob’s curve). Bob sends Alice his curve, and Alice sends Bob hers. Alice then starts the random again from EB, and repeats her random walk. Bob starts his walk from EA and repeats his random walk, and then eventually meet at a new secret curve (ES). This will be a curve which is only known to them, and they can use this to create a new key, as no one else will know this curve, unless they know both Bob and Alice’s random walk.

Rather than use elliptic curves, let’s just prove this will a simple linear equation. Let’s say that Bob and Alice start with:

y = 4x + 3

Bob now takes a walk of (x+2), and will end up with:

yB = 4 (x+2) + 3 = 4x + 11

Alice now takes a walk of (x-3) and will send up with:

yA = 4 (x-3) + 3 = 4x-9

Bob gets yA, and takes the same walk (x+2) and gets:

kB = 4 (x+2) — 9 = 4x -1

And Alice get yB, and takes the same walk (x-3) and gets:

kA = 4 (x-3) + 11 = 4x -1

and thus Bob and Alice have the same linear equation, and if they take a value of x, they will end up with the same key.

You can find out more about SIKE here:

https://asecuritysite.com/pqc/sike

So What’s The Problem With SIDH?

Just last year, Craig Costello published a paper on the 10 years of SIKE (and where SIKE is the core foundation for SIDH):

It has a classic quote about it being relatively new and that it had been only 10 years since Jao and De Feo published the SIDH protocol [1]. Within the paper, too, Craig outlined areas of attack on SIDH:

In the second paragraph, we see an attack on SIDH using “endomorphism ring of the starting curve”, and which is the basis of the attack defined in the new paper. Craig also outlines a possible “tweak” for this type of attack. It is thus possible that we need to create starting curves that are more randomized — but this will have a performance hit on SIDH. If this tweak is possible, it will be a fairly easy fix for the SIDH method, but may have a significant effect on its performance.

A note about performance

It is well known that isogeny-based methods perform less well than lattice ones. In the tests I conducted, we see that SIDH performs weakly against Kyber, with it being over 100 times slower for key generation, encapsulation and decapsulation [here]:

But, research generally comes up with improved methods. With ECC, we saw the performance of a scalar operation on the P-256 curve go from over 2 million cycles to less than 60,000 cycles in just a decade of research work [1]:

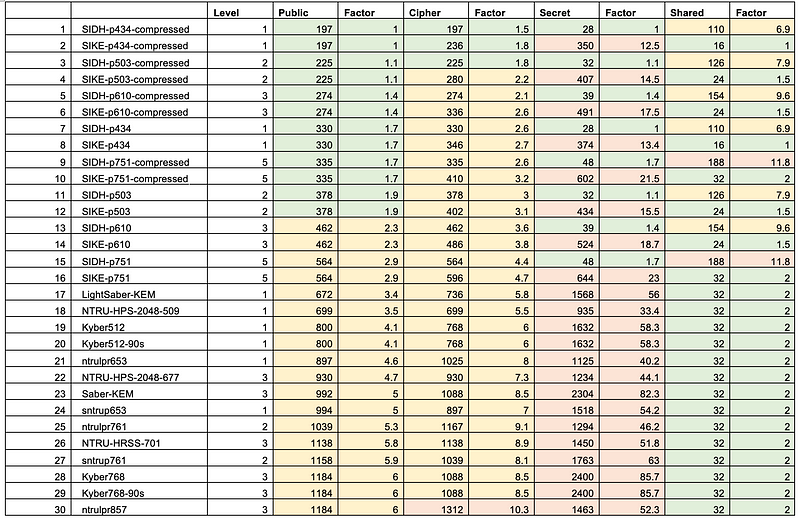
A core advantage of isogenies is that it produces small keys and ciphers. In the following we see that level 1 (p434) produces a public key of 197 bytes and a secret key of just 28 bytes, as opposed to Kyber which has a public key of 800 bytes and a secret key of 768 bytes [here]:

Conclusion

Without the full paper, it is difficult to know if this is a new attack or one based on previously defined (and well-known) methods. One thing that is likely is that the performance levels for SIDH will drop and that we need to improve our core methods for generating isogenies. If it is broken, then fine, as it’s better to know now than in the future when real systems are built on the methods. What’s likely, is that the tweak defined in Craig’s paper might be the solution. We should, though, pause any deployment of SIDH until a fix is found.

Overall, I am so happy to be part of this amazing research environment. Long live isogenies (possibly)!

References

[1] De Feo, L., Kieffer, J., & Smith, B. (2018, December). Towards practical key exchange from ordinary isogeny graphs. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 365–394). Springer, Cham.

[2] Costello, C. (2021). The case for SIKE: a decade of the supersingular isogeny problem. Cryptology ePrint Archive.

[3] Castryck W and Decru T (2022), An efficient key recovery attack on SIDH (preliminary version, Cryptology ePrint Archive, Paper 2022/975 [here].