Paranoid Cryptography: ROCA

I have been investigating a new library from Google, and which analyses a range of vulnerabilities within cryptography [here]:
Photo by Sixteen Miles Out on Unsplash

Paranoid Cryptography: ROCA

I have been investigating a new library from Google, and which analyses a range of vulnerabilities within cryptography [here]:

One of the tests relates to the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key [article]. It has the CVE identifier of CVE-2017–15361. It was found in the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware and affected BitLocker with TPM 1.2 and YubiKey 4.

With this the library was slopping in creating prime numbers, and rather than generating them randomly, it generated from

and where k and a are generated randomly. In RSA, these are then multiplied to produce an RSA modulus:

N=p.q

From the modulus, it is then relatively easy to factorize back to p and q, and then easy to crack the RSA method.

ROCA

The attack focuses on using the Coppersmith method [2] to factorize the module, and where the research team — through responsible disclosure — were able to factorize the prime numbers and without gaining access to RSALib [1]:

Overall the research team verified the cracking of 512-bit RSA keys within less than two hours and keys within 97 days (and at a cost of around $76 per crack on the Amazon AWS Cloud). These were achieved on a standard processor and could be considerably reduced on multi-process systems [1]:

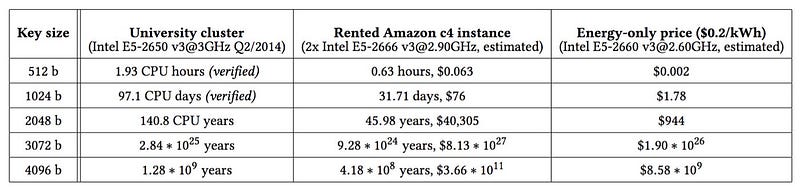
As we see 2,048-bit keys (the current recommended size) take over 140 years on a single and will cost over $40,000 for a single crack. At the core of the crack is the availability of the public key, as some of the bits of the key make it easier for the system to find the factors. For TLS and PGP it is relatively easy as the keys must be known, but for payment cards and electronic IDs, it is less easy:

In the research, the team assessed a wide range of datasets and found that the Estonian ID system and some TPM chips were highly vulnerable:

Detecting ROCA

The paper outlines the basic method of:

To produce our weak keys, we need to create a product of primes:

def product_of_primes(nprimes):  
    product_of_primes=1
    if (nprimes>len(PRIMES)): nprimes=len(PRIMES)
    for i in range(0,nprimes):
        product_of_primes *= primes[i]
    return product_of_primes

In order to detect ROCA, we determine if there is a discrete log of a value for a log of 65,537 (mod N):

def _HasDiscreteLog(value, base, n):
    b = base % n
    accumulator = 1
    for unused_exponent in range(1, n):
      if accumulator == value:
        return True
      accumulator = (accumulator * b) % n
    return False
def IsWeak(modulus,nprimes):
    mod_product_of_primes = modulus % product_of_primes_val
    for i in range(0,nprimes):
        mod_p = mod_product_of_primes % primes[i]
        if not _HasDiscreteLog(mod_p, F4, primes[i]):
            return False
    return True

Coding

The following is an outline of the code [here]:

import random
import sys
PRIMES = primes = (2,3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999)
def product_of_primes(nprimes):  
    product_of_primes=1
    if (nprimes>len(PRIMES)): nprimes=len(PRIMES)
    for i in range(0,nprimes):
        product_of_primes *= primes[i]
    return product_of_primes
def _HasDiscreteLog(value, base, n):
    b = base % n
    accumulator = 1
    for unused_exponent in range(1, n):
      if accumulator == value:
        return True
      accumulator = (accumulator * b) % n
    return False
def IsWeak(modulus,nprimes):
    mod_product_of_primes = modulus % product_of_primes_val
    for i in range(0,nprimes):
        mod_p = mod_product_of_primes % primes[i]
        if not _HasDiscreteLog(mod_p, F4, primes[i]):
            return False
    return True
F4 = 0x10001
nprimes=20
if (len(sys.argv)>1):
    nprimes=int(sys.argv[1])
print("Number of primes used=",nprimes)
print(f"For p, k={k}, a={a}")
     
a=random.randint(1,10)
k=random.randint(1,10)
product_of_primes_val=product_of_primes(nprimes)
p = k*product_of_primes_val+pow(65537,a,product_of_primes_val)
a=random.randint(1,10)
k=random.randint(1,10)
print(f"For q: k={k}, a={a}")
q =k*product_of_primes_val+pow(65537,a,product_of_primes_val)
n=p * q 

print("\nN=",n)
print("p=",p)
print("q=",q)
if IsWeak(n,nprimes):
    print("Key is weak")

A sample run is [here]:

Number of primes used= 39
For p, k=7, a=8
For q: k=10, a=5
N= 64908741457145883358850701100615095578223493084762239607579753897494592072619278526488374890039885274779916897439019301672653242339327
p= 6740631945151887489398623511648264911889196907864482099045784584811
q= 9629474207359839270569462159011344291964192515080186903950074484157
Key is weak

Conclusions

One of the most costly cybersecurity attacks is a breach of the trust infrastructure. This typically involves the discovery of a secret key. Testing for ROCA is just one approach to making sure you are generating safe RSA keys. Here is the ROCA detection method here:

https://asecuritysite.com/rsa/rsa_02

References

[1] Nemec, M., Sys, M., Svenda, P., Klinec, D., & Matyas, V. (2017, October). The return of coppersmith’s attack: Practical factorization of widely used rsa moduli. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (pp. 1631–1648).

[2] Coppersmith, D. (1996, May). Finding a small root of a univariate modular equation. In International Conference on the Theory and Applications of Cryptographic Techniques (pp. 155–165). Springer, Berlin, Heidelberg.