Crypto Magic: Recovering Alice’s Public Key From An ECDSA Signature

Crypto Magic: Recovering Alice’s Public Key From An ECDSA Signature
The core of the security of the Internet is based on one thing: PKI (Public Key Infrastructure). With this, Alice has a key pair: a public key and a private key. This can either be an RSA key pair or an Elliptic Curve key pair. If Alice wants to prove her identity and a message, she signs a hash of the message with her private key, and then Bob can prove this with her public key. Two of the most common signing methods are RSA and ECDSA (Elliptic Curve Digital Signature Algorithm). But, how can Bob know that Alice’s public key is correct? Well, this is where PKI comes in. With this Trent — an entity trusted by Bob and Alice — takes Alice’s public key and does his own signs it with his own private key. When Bob receives this signed public key, he checks it against Trent’s public key and will validate this it is Alice’s public key. And everything is fine.
But, why do we even have PKI? Why do we need Trent? Why does Alice have to go to Trent to get a signed version of her keys? Why can’t Alice just produce her key pair, and for Bob to discover her public key from her transactions? Well, with Bitcoin and Ethereum, we don’t need Trent anymore, as anyone can discover Alice’s public key, and validate the transaction. Within Bitcoin and Ethereum, a version of Alice’s public key becomes her public key identity.
Recovering Alice’s public key without needing Trent
So, let’s recover Alice’s public key from just one signature. In ECDSA, Bob creates a random private key (x), and then a public key from:

Next, in order to create a signature for a message of M, he creates a random number (k) and generates the signature of:
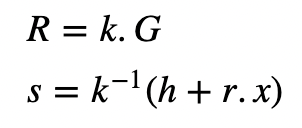
and where x is the private key and h=H(M) The signature is then (r,s) and where r is the x-coordinate of the point kG. h is the SHA-256 hash of the message (M), and converted into an integer value. Now, we need to recover the public key from (R,s). For this, we take:

and transform to give:

Now, we take:
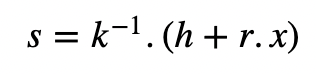
and substitute k to give:

And thus:

And so we have found the public key:

As we can get two y co-ordinate points, we also get:
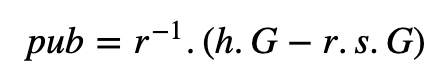
Both these points will have the same x-coordinate point, and which is equivalent of having (x,y) and (x,−y).
Coding
The coding becomes the operations of point addition, scalar multiplication, and in creating the negative of a point:
pub = scalar_mult(libnum.invmod(r,curve.n),(point_add(scalar_mult(s,rpoint),point_neg(scalar_mult(h,curve.g)))))
and which is translated to:

and which is:

with this, R is the the value of r converted to a point (r.G). With this, R is the value of r converted to a point (r.G). In this case, G is the base point on the curve. We can code this with [here]:
import sys
import random
import hashlib
import libnum
from secp256k1 import curve,scalar_mult,point_add,point_neg
msg="Hello"
if (len(sys.argv)>1):
msg=(sys.argv[1])
# Alice's key pair (dA,QA)
dA = random.randint(0, curve.n-1)
QA = scalar_mult(dA,curve.g)
h=int(hashlib.sha256(msg.encode()).hexdigest(),16)
k = random.randint(0, curve.n-1)
rpoint = scalar_mult(k,curve.g)
r = rpoint[0] % curve.n
# Bob takes m and (r,s) and checks
inv_k = libnum.invmod(k,curve.n)
s = (inv_k*(h+r*dA)) % curve.n
print (f"Msg: {msg}\n\nAlice's private key={dA}\nAlice's public key={QA}\nk= {k}\n\nr={r}\ns={s}")# To check signature
inv_s = libnum.invmod(s,curve.n)
c = inv_s
u1=(h*c) % curve.n
u2=(r*c) % curve.n
P = point_add(scalar_mult(u1,curve.g), scalar_mult(u2,QA))
res = P[0] % curve.n
print (f"\nResult r={res}")
if (res==r):
print("Signature matches!")
print("\n=== Now recovering Alice's public key ===")
pub1 = scalar_mult(libnum.invmod(r,curve.n),(point_add(scalar_mult(s,rpoint),point_neg(scalar_mult(h,curve.g)))))
pub2 = scalar_mult(libnum.invmod(r,curve.n),(point_add(point_neg(scalar_mult(s,rpoint)),scalar_mult(h,curve.g))))
print(f"\nAlice's public key is one of the these:\n{pub1}\n{pub2}")
if (pub1[0]==QA[0]):
print("Key recovered")And a sample run [here]:
Msg: Hello
Alice's private key=51807341738254329389736646254693242327142174011095991939024161233563883052655
Alice's public key=(29536825323447158318398958334778222234623534948898819523892551224271187751503, 100617733002231258870267900359120638387481820412279399098395797030288659404861)
k= 78239816292540973623348822290723524828665027578289616038455379559013972694565
r=91457593152987843762518269128415380901655617003136377539774416188614535938789
s=94829889541214320331845482826979126529774337950845442366439736640766059212081
Result r=91457593152987843762518269128415380901655617003136377539774416188614535938789
Signature matches!
=== Now recovering Alice's public key ===
Alice's public key is one of these:
(29536825323447158318398958334778222234623534948898819523892551224271187751503, 100617733002231258870267900359120638387481820412279399098395797030288659404861)
(29536825323447158318398958334778222234623534948898819523892551224271187751503, 15174356235084936553303084649567269465788164253361164941061786977620175266802)
Key recovered
And, that’s it. We have recovered Alice’s public key from just one ECDSA signature.
Conclusions
While PKI has secured the Internet, it is still a centralised approach to trust and where keys can easily be revoked. It depends on the core root trust providers, such as Google, DigiCert, GoDaddy, and so on. In a distributed ledger approach, the trust comes from the ownership of a private key, and where there is no need for Trent anymore. Overall, we are not going to move from PKI any time soon for our trust, but for many application areas, the usage of wallets is a more distributed and citizen-centric approach to trust.
And, so, here’s the magic: