Does ElGamal Encryption Do A Homomorphic Addition?

Does ElGamal Encryption Do Homomorphic Addition and Subtraction?

Well, yes, but with a small modification …

Homomorphic encryption provides us with a way to encrypt values and then to be able to process them. Let’s say we have Bob the Data Processor and Alice the Consumer. With this, Alice could encrypt the values that she has with her public key, and then Bob can process these values with mathematical operations and then give the result back to Alice, who will then decrypt the result.

For given methods, such as for RSA and ElGamal, we can have partial homomorphic encryption (PHE), and where we implement a few of the arithmetic operations. For example, ElGamal naturally supports multiplication and division:

https://asecuritysite.com/elgamal/el_homomorphic01

But what about addition and subtraction? Well, with a tweak, we can modify ElGamal to support addition and subtraction.

Homomorphic addition using the ElGamal method

With ElGamal encryption, initially, Bob creates his public key by selecting a g value and a prime number (p) and then selecting a private key (x). He then computes Y which is:

His public key is (Y,g,p) and he will send this to Alice. Alice then creates a message (M) and selects a random value k. She then computes a and b:

Bob then receives these and decrypts with:

This works because:

Now with additive homomorphic encryption, we change the encryption to be:

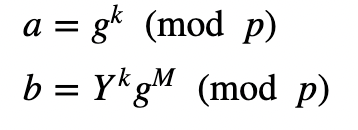
Notice that instead of:

we now have:

The result of the decryption then gives:

Then just need to brute force the resulting value to find a value which matches g^i. The working out is:

and then:

The modification (for values of v1 and v2) is simply [here]:

k1=random.randrange(3, p)  
a1=pow(g,k1,p)
b1=(pow(Y,k1,p)*pow(g,v1,p)) % p

k2=random.randrange(3, p)  
a2=pow(g,k2,p)
b2=(pow(Y,k2,p)*pow(g,v2,p)) % p

We then search the result for possible values of M1+M2. An example of a search for the solution to v_r is [here]:

for i in range(1,2**bits):
    if (pow(g,i,p)==v_r):
        print("Found: ",i)
        break

One of the great advantages of using Python is that it automatically deals with Big Integers. We thus do not need any special data type and can just operate on them as if they were normal integer types. The coding is [here]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import random
import libnum
import sys
import hashlib
    
def get_generator(p: int):
    while True:
        # Find generator which doesn't share factor with p
        generator = random.randrange(3, p)
        if pow(generator, 2, p) == 1:
            continue
        if pow(generator, p, p) == 1:
            continue
        return generator
    
bits=512
v1=10
v2=5

if (len(sys.argv)>1):
    v1=int(sys.argv[1])
if (len(sys.argv)>2):
    v2=int(sys.argv[2])
if (len(sys.argv)>3):
    bits=int(sys.argv[3])

p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
    
        
g = get_generator(p)  
x = random.randrange(3, p)  
Y = pow(g,x,p)

print (f"v1={v1}\nv2={v2}\n")
print (f"Public key:\ng={g}\nY={Y}\np={p}\n\nPrivate key\nx={x}")

k1=random.randrange(3, p)  
a1=pow(g,k1,p)
b1=(pow(Y,k1,p)*pow(g,v1,p)) % p

k2=random.randrange(3, p)  
a2=pow(g,k2,p)
b2=(pow(Y,k2,p)*pow(g,v2,p)) % p

a=a1*a2
b=b1*b2

print (f"\nEncrypted (v1)\na={a1}\nb={b1}")
print (f"\nEncrypted (v2)\na={a2}\nb={b2}")
print (f"\nAfter homomorphic encryption\na={a}\nb={b}")

v_r=(b*libnum.invmod(pow(a,x,p),p)) % p

print ("\nResult: ",v_r )

# Now search for g^i
for i in range(1,2**bits):
    if (pow(g,i,p)==v_r):
        print("Found: ",i)
        break

A sample run for 60-bit primes and adding 100 and 20 [here]:

v1=100
v2=20

Public key:
g=528317843179741300
Y=448827185772177630
p=649287730900795799

Private key
x=266162610601557224

Encrypted (v1)
a=20899511822881218
b=375223311470810657

Encrypted (v2)
a=342523487251239679
b=495029915104300524

After homomorphic encryption
a=7158573671421787817804548065449022
b=185746764022549912519224917229884268

Result:  366204065039618358
Found:  120

Subtraction

For subtraction, we modify with:

A demo for subtraction is here:

https://asecuritysite.com/elgamal/el_homomorphic04

Conclusions

ElGamal methods are now being used in a range of homomorphic and zero-knowledge proof methods and are generally much less processor intensive than fully homomorphic encryption (FHE) methods. If you want to know more about ElGamal encryption, try here:

https://asecuritysite.com/elgamal/

and for homomorphic encryption here:

https://asecuritysite.com/homomorphic/