Homomorphic Encryption with ElGamal Using Python (Multiplication and Division)

We live in a 20th Century world of data, and where often do not protect our data. In a future data world, all of our values could be…
Photo by Sander Sammy on Unsplash

Homomorphic Encryption with ElGamal Using Python (Multiplication and Division)

We live in a 20th Century world of data, and where often do not protect our data. In a future data world, all of our values could be encrypted, and where we can still operate on them. This will be a world of homomorphic encryption.

Meet Taher Elgamal

Taher Elgamal is one of the giants of cybersecurity. His work on Netscape led to the creation of SSL, and on which much of our Web security is still built on. Along with this, he published this paper in 1985 [here]:

It was true classic and has been referenced over 11,700 times. Within the paper, Tahir outlined an encryption method and a digital signature method. His ‘base’ was to take John Napier’s logarithms, and make them discrete. This discrete element meant that we only dealt with positive integer values and where we worked within a finite field. This field was defined by a prime number (p).

While the core ElGamal encryption method was overtaken in its usage by RSA, and then by ECC (Elliptic Curve Cryptography), the signature method was adopted as the Digital Signature Standard (DSS) by NIST. This has since scaled into ECC to become ECDSA, and which is used by Bitcoin and Ethereum.

Applying ElGamal encryption to homomorphic encryption

With homomorphic encryption, we can mathematically operate on values. For example, we can encrypt the value of 5, and the value of 4, and then multiply the encrypted values, and when we decrypt, we will get a value of 20. Thus, we can encrypt two values (a and b) with a public key (pk):

and then multiply the ciphered values to give a result C):

Then, when we decrypt C with the private key (sk), and we should get the multiplication of a and b:

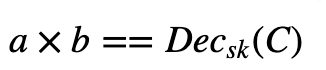
With ElGamal encryption, initially Bob creates his public key by selecting a g value and a prime number (p) and then selecting a private key (x). He then computes Y which is:

His public key is (Y,g,p) and he will send this to Alice. Alice then creates a message (M) and selects a random value k. She then computes a and b:

Bob then receives these and decrypts with:

his works because:

To multiply homomorphically, we generate a unique k value for each encryption (k_1 and k_2):

Then we get:

We can see that M will equal M_1 times M_2.

Coding

One of the great advantages of using Python is that it automatically deals with Big Integers. We thus do not need any special data type and can just operate on them as if they were normal integer types. The coding is here [coding]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import random
import libnum
import sys
import hashlib
    
def get_generator(p: int):
    while True:
        # Find generator which doesn't share factor with p
        generator = random.randrange(3, p)
        if pow(generator, 2, p) == 1:
            continue
        if pow(generator, p, p) == 1:
            continue
        return generator
    
bits=512
v1=10
v2=5
if (len(sys.argv)>1):
    v1=int(sys.argv[1])
if (len(sys.argv)>2):
    v2=int(sys.argv[2])
if (len(sys.argv)>3):
    bits=int(sys.argv[3])
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
    
        
g = get_generator(p)  
x = random.randrange(3, p)  
Y = pow(g,x,p)
print (f"v1={v1}\nv2={v2}\n")
print (f"Public key:\ng={g}\nY={Y}\np={p}\n\nPrivate key\nx={x}")
k1=random.randrange(3, p)  
a1=pow(g,k1,p)
b1=(pow(Y,k1,p)*v1) % p
k2=random.randrange(3, p)  
a2=pow(g,k2,p)
b2=(pow(Y,k2,p)*v2) % p
a=a1*a2
b=b1*b2
print (f"\nEncrypted (v1)\na={a1}\nb={b1}")
print (f"\nEncrypted (v2)\na={a2}\nb={b2}")
print (f"\nAfter homomorphic encryption\na={a}\nb={b}")
v_r=(b*libnum.invmod(pow(a,x,p),p)) % p
print ("\nResult: ",v_r )

A sample run for 60-bit primes and with 5x34 is [here]:

v1=5
v2=34
Public key:
g=41037222245906045
Y=143759851511551134
p=954335099446898089
Private key
x=28874735387014000
Encrypted (v1)
a=268639169963660252
b=656796225640099477
Encrypted (v2)
a=941561210902047398
b=631628053618644943
After homomorphic encryption
a=252940222166704867168624404872624296
b=414850921625128374957562760462994811
Result:  170

and for 512-bit primes [here]:

v1=5
v2=34
Public key:
g=6543044051683815102229925148798636299331503948917227000793415250303481305291781956653105323139870360854743208856483686869029384572766044204700871486141555
Y=1921267984988116088826677855875133320719426972148295176448176228940131899844438116197684832477305259416013723092655113523719022436859771465809253940438757
p=9636597738737678510729553708369548460708981116185911518340246978255707014090872937837973136081683813672204343480079959725789060282195196906226025043320663
Private key
x=3603207254020055235950706217980221513336115533367798659375744848896180287031286459369453086495985287414224201940840213304736755087919213064145005148905968
Encrypted (v1)
a=6490135599785296929332463948775620147790247670036964508973292944016160330995859964508608777871403231758116938286634499109595024988153801904525210409034012
b=2564179155946911798761123347893169670242199453427541967695233031796606102515614902070854234860935975982235659076786700581323058649718236071505712670656492
Encrypted (v2)
a=9090438183111126521232890295853263270766996949666018452885200943561524122147070582875487016585818749849990430055258201917745206314207621994652235118736298
b=4886026557032758639237454523272917632112370880840808221871302740780423396132561147870107687586105565804427799421564595338223896082726350646025793789398291
After homomorphic encryption
a=58998176469857095999930360976091347130090887017276797297243682239760959001274375801673443926760489632582893710676750087288668265275833131495854281719924077471058723462113642122290039430531416892699861728174678179676558582966473037548603235605979862694462065083539341196448235487619258565069158456584340967576
b=12528647452946454550793353902800959552749246399067344589404470803480268972485105732444279740168350400125277538497934025673783100992817132714362225482542804386030314076779649147552138003036231905397677988937881101159203160750239886739230010565959145291878235469144522255611916961021605436371453851436632855172
Result:  170

Some examples are here:

  • Val1=9, Val2=3. Test
  • Val1=300, Val2=6. Test
  • Val1=30000, Val2=6. Test
  • Val1=50400, Val2=2. Test
  • Val1=6540365, Val2=5. Test

Homomphonic Division

For division, we take the inverse of the values:

This is implemented as an inverse mod p operation:

a=a1*libnum.invmod(a2,p)
b=b1*libnum.invmod(b2,p)

Some samples of this are here:

  • Val1=9, Val2=3. Test
  • Val1=300, Val2=6. Test
  • Val1=30000, Val2=6. Test
  • Val1=50400, Val2=2. Test
  • Val1=6540365, Val2=5. Test

Conclusions

And that’s it … some partial homomorphic encryption for ElGamal. Overall, in some circumstances, we might only want multiplication or division for our homomorphic encryption, so this ElGamal method can be fast and efficient.