So What Are dQ, dP, and InvQ Used For In RSA?

If you look at a private key in RSA, you will see p and q — the core prime numbers, and the modulus N (and which is p times q). But you…

So What Are dQ, dP, and InvQ Used For In RSA?

If you look at a private key in RSA, you will see p and q — the core prime numbers, and the modulus N (and which is p times q). But you will also see dQ, dP and InvQ. Overall, they make the decryption process faster and use Chinese Remainer Theorem.

Chinese Remainder Theorem (CRT) and RSA

With the Chinese Remainder Theorem (CRT), we can solve:

x (mod 16) = 7
x (mod 14) = 13
x (mod 12) = 7

and which gives a solution of x=55. Overall, CRT is used in many examples of cracking ciphers, but it can also be used to enhance performance. With RSA, we create two random prime numbers (p and q), and determine the modulus:

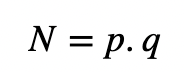
We then encrypt a message with:

and decrypt with:

and where (e,N) is the encryption key, and (d,N) is the decryption key. Unfortunately, C^d is a fairly complex operation, so can we simplify it?

dP, dQ and InvQ

In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve:

For this we need:

and which is the inverse of e mod (p-1). Also:

and:

The message is then recovered using less complex operations of:

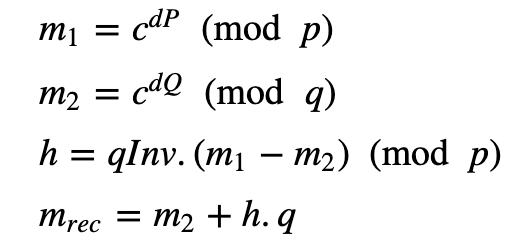
This operation can be up to four times faster than performing M=C^d (mod N).

Coding

The coding is [here]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import sys
import libnum

msg="Hello"
bits=256

if (len(sys.argv)>1):
    msg=str(sys.argv[1])
if (len(sys.argv)>2):
    bits=int(sys.argv[2])

m=  bytes_to_long(msg.encode())

p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)

N=p*q
e=65537
PHI=(p-1)*(q-1)
d=libnum.invmod(e,PHI)
c=pow(m,e,N)

dP = 1 * pow(e,-1,p-1)
dQ= 1 * pow(e,-1,q-1)
qInv= 1 * pow(q,-1,p)

m1 = pow(c,dP,p)
m2 = pow(c,dQ,q)
h = (qInv*(m1 - m2)) % p
m_rec = m2 + h*q

print(f"Msg={msg}\nbits={bits}")
print(f"p={p}\nq={q}")
print(f"N={N}\n")
print(f"C={c}\n")
print(f"dP={dP}\n")
print(f"dQ={dQ}\n")
print(f"qInv={qInv}\n")

print(f"Recovered message: {long_to_bytes(m_rec).decode()}")

and a sample run for 256-bit prime numbers is [here]:

Msg=hello
bits=256
p=83385232790227163445814758633988455715592790482281989757036568486927737484359
q=98456521431402396778792139066485154337839503139303201433503199439442486152931
N=8209819959273478594234820651623149738207753181630251673715134869672761810238097757820289073916959058695204513214118093006212638798981882197450897694506229

C=1805172009424128756584171834316132474603196173088996038963614900087417379407174707336783594500350445868931380578377336606603821942282761031362891099621260

dP=34102482482818234918262553605853068931214940618224883217996721625267011730675

dQ=90142769053335337502752105229203483768457263940485679778056555471945122551143

qInv=67479617748248419862673762090264580282073583656235872628170386242300886582027

Message: hello

Conclusions

CRT are used in many cracking examples, but they can also be used for good. Here’s an example:

https://asecuritysite.com/rsa/rsa_crt3