Beware of RSA Fault Attacks — They May Comprise Your Trust Infrastructure

In a brilliant paper published at USENIX 2022, Sullivan et al [1] show that real-life RSA signatures can be cracked for their private key…
Photo by Thomas Dumortier on Unsplash

Beware of RSA Fault Attacks — They May Comprise Your Trust Infrastructure

In a brilliant paper published at USENIX 2022, Sullivan et al [1] show that real-life RSA signatures can be cracked for their private key — if the signature contains a fault. In a previous article, I outlined how faults in ECDSA can cause compromises:

https://medium.com/asecuritysite-when-bob-met-alice/ecdsa-signatures-can-be-cracked-with-one-good-signature-and-one-bad-one-2d8bc71949e9?sk=b2d77913f1420d2a72952c1f2395d379

Now, we will look at RSA faults. Overall, the RSA fault attack has been known for a while, and it was Lenstra [2] and Bohen et al [3] who outlined how the method recovers the prime numbers (p and q) used in RSA. Once these are revealed, it is then trivial to generate the private key:

The RSA fault attack basically focuses on a fault occurring in the generation of the signature using RSA-CRT (Chinese Remainder Theory).

RSA and CRT

With RSA, we create two random prime numbers (p and q), and determine the modulus:

We create a signature of a message with:

and where (e,N) is the encryption key, and (d,N) is the decryption key. In order to create the signature we can apply CRT (Chinese Remainder Theory) to solve:

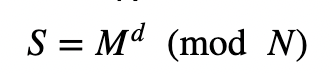
For this we use CRT to solve for M in:

and also use Fermat’s Little Theorem:

For this we need:

and which is the inverse of e \pmod {p-1}. Also:

and:

The signature is then created using less complex operations of:

This operation can be up to four times faster than performing S=M^d (mod N).

Adding a Fault

The implementation of the code above is:

e=65537
dP = 1 * pow(e,-1,p-1)
dQ= 1 * pow(e,-1,q-1)
qInv= 1 * pow(q,-1,p)
s1 = pow(m,dP,p)
s2 = pow(m,dQ,q)
h = (qInv*(s1 - s2)) % p
s= s2 + h*q

But now let’s introduce a fault in s_1 or s2, and which will then produce an incorrect signature (s). If we do it on s2, then:

e=65537
dP = 1 * pow(e,-1,p-1)
dQ= 1 * pow(e,-1,q-1)
qInv= 1 * pow(q,-1,p)
s1 = pow(m,dP,p)
s2 = pow(m,dQ,q)+1 
h = (qInv*(s1 - s2)) % p
s= s2 + h*q

Notice that s2 has one added to it. We can first recover p with:

and where GCD is the greatest common denominator. This will work, as p is correct and will still share a factor in the faulty signature. To determine q, we can simply divide N by the recovered p value. We can then recover p and q using:

p_rec=libnum.gcd(pow(s,e,N)-m,N)
q_rec = N//p_rec

Coding

The coding is [here]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import sys
import libnum
msg="Hello"
bits=256
if (len(sys.argv)>1):
    msg=str(sys.argv[1])
if (len(sys.argv)>2):
    bits=int(sys.argv[2])
m=  bytes_to_long(msg.encode())
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
N=p*q
e=65537
dP = 1 * pow(e,-1,p-1)
dQ= 1 * pow(e,-1,q-1)
qInv= 1 * pow(q,-1,p)
s1 = pow(m,dP,p)
s2 = pow(m,dQ,q)+1 # Add an error
h = (qInv*(s1 - s2)) % p
s= s2 + h*q
p_rec=libnum.gcd(pow(s,e,N)-m,N)
q_rec = N//p_rec
print("s1 (no error): ",s1)
print("s2 (error): ",s2)
print("s (error): ",s)
print("p recovered: ",p_rec)
print("q recovered: ",q_rec)
if (p==p_rec): print("!!! Successfully recovered p !!!")
if (q==q_rec): print("!!! Successfully recovered q !!!")
print(f"\n\nMsg={m}\nbits={bits}")
print(f"p={p}\nq={q}")
print(f"N={N}\n")
print(f"M={m}\n")
print(f"dP={dP}\n")
print(f"dQ={dQ}\n")
print(f"qInv={qInv}\n")
# print(f"Message: {long_to_bytes(m_rec).decode()}")

and a sample run for 256-bit prime numbers is [here]:

s1 (no error):  56021528294969193000731306253734117928622714863840906998488964544710659710980
s2 (error):  42724684149461483152909999694448356241172489949685162384842906716939741826064
s (error):  6469101265404271060291683786345788979042545758481144741828344290809928816661412935473574653422845058112228879641634752200930385344983247751270281428653036
p recovered:  97517551883295679149151625389578232227330410834441262164393827490010395338679
q recovered:  89616351945908038439087976457740417907961251495093633980856593171428370490021
!!! Successfully recovered p !!!
!!! Successfully recovered q !!!

Msg=448378203247
bits=256
p=97517551883295679149151625389578232227330410834441262164393827490010395338679
q=89616351945908038439087976457740417907961251495093633980856593171428370490021
N=8739167250476772834723958776533490857578332452121827595533332412376015002357767538111398114928439814548573718893487586591637049018866157094722857484822259
M=448378203247
dP=58431370750951951180371930015462221360987501763243266001397397068910969598159
dQ=31373996048749775454269108012975817453961318862679529701645996516856928643713
qInv=71254943511234361046555380686031562560199917601477871414869197304782914474460

Conclusions

If you have time, please give the paper a read [1]. The RSA fault attack demo is here:

https://asecuritysite.com/rsa/rsa_fault

and for ECDSA, it is here:

https://asecuritysite.com/ecdsa/ecd7

References

[1] Sullivan, G. A., Sippe, J., & Wustrow, E. (2022). Open to a fault: On the passive compromise of {TLS} keys via transient errors. In 31st USENIX Security Symposium (USENIX Security 22) (pp. 233–250).

[2] Lenstra, A. K. (1996). Memo on RSA signature generation in the presence of faults (No. REP_WORK).

[3] Dan Boneh, Richard A. DeMillo, and Richard J. Lipton.
On the importance of eliminating errors in cryptographic
computations. Journal of Cryptology, 14(2):101–119,
March 2001.