RSA Is Alive And Kicking in Nearly Every TLS Connection: Creating Fast RSA Signatures

While elliptic curve methods have taken over with key exchange and in digital signing with Bitcoin and Ethereum, the RSA signature method…
Photo by Everyday basics on Unsplash

RSA Is Alive And Kicking in Nearly Every TLS Connection: Creating Fast RSA Signatures

While elliptic curve methods have taken over with key exchange and in digital signing with Bitcoin and Ethereum, the RSA signature method is still one of the most popular methods for signing. Sullivan et al [1], for example, found that ECDHE with RSA was by far the most popular way of authenticating the key exchange in TLS sessions (with over 90% of all the signatures):

The ECDHE_RSA method is where we use elliptic curve methods for the key exchange, and then authenticate the server in this exchange with either RSA or ECDSA signing. Overall, RSA public keys are by far the most popular method of providing a public key on the Internet, and most sites have an RSA public key, and thus use this key to sign the key exchange.

But, we have a slight problem. The key size of RSA has increased over the years, and has a much larger processing footprint than ECC. How can we improve the performance of signing in RSA? Well, we turn to the Chinese Remainder Theorem (CRT).

RSA Signing with CRT

With RSA, we create two random prime numbers (p and q), and determine the modulus:

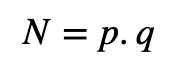
We sign a message (M) with the private key (d,N):

and check the signature with the public key (e,N):

and where (e,N) is the encryption key, and (d,N) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve:

For this we use CRT to solve for S in:

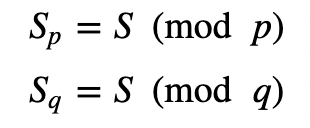
and also use Fermat’s Little Theorem:

For this we need:

and which is the inverse of e for mod(p-1). Also:

and:

The signature is then recovered using less complex operations of:

This operation can be up to four times faster than performing:

Testing CRT

So, now let’s create some code, and run a real-life experiment. The coding is [here]:

from Crypto.Util.number import *
from Crypto import Random
import Crypto
import sys
import libnum
import time
msg="Hello"
bits=256
if (len(sys.argv)>1):
    msg=str(sys.argv[1])
if (len(sys.argv)>2):
    bits=int(sys.argv[2])
m=  bytes_to_long(msg.encode())
p = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
q = Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
N=p*q
e=65537
PHI=(p-1)*(q-1)
d=libnum.invmod(e,PHI)
dP = 1 * pow(e,-1,p-1)
dQ= 1 * pow(e,-1,q-1)
qInv= 1 * pow(q,-1,p)
t0 =  time.time()
s1 = pow(m,dP,p)
s2 = pow(m,dQ,q)
h = (qInv*(s1 - s2)) % p
s_crt= s2 + h*q
delta1 = time.time() - t0

t0 = time.time()
s_d=pow(m,d,N)
delta2 = time.time() - t0

print(f"Msg={msg}\nbits={bits}")
print(f"p={p}\nq={q}")
print(f"N={N}\n")
print(f"Msg={msg}\n")
print("== Signature using CRT ===")
print(f"dP={dP}\n")
print(f"dQ={dQ}\n")
print(f"qInv={qInv}\n")
print(f"s1={s1}\n")
print(f"s2={s2}\n")
print(f"s_crt={s_crt}\n")
print("== Signature using (d,N)) ===")
print(f"s_d={s_d}\n")
if (s_crt==s_d): print("\nThe signatures are the same!!!")
print (f"Time with CRT = {delta1} Seconds")
print (f"Time Traditional = {delta2} Seconds")

and a sample run for 738-bit prime numbers is [here]:

Msg=hello
bits=768
p=865176729431424337158429417935450045433092389674648134690338126923127805096555697325910525407029344746053545614106711855820855719844880577204614383112404586572107063986774424558542018523002454940905139753945284705328299197062712169
q=919069557362574850817978672390371199448727235884709313327317318873549197349887568114287361492392820698287637186604747259870164380085366268182103468997477607321491623718098750657077026372611348214105429755216807021331167445129401911
N=795157593758939351036001740812628772275959623636171723352046230350302217806979586835539003264241373640575942785760109055933787119543048729281162366881652630796555755887813986113597646932594926430102997375640448463770715237606892171320424416022774352147414355454122742802016813448375640158040994474593705125409235950028624687253103752571538067919845848950453756347732957208885812158906545307446169910424522151350900198112831765068787532136702241257818746511554959
Msg=hello
== Signature using CRT ===
dP=133637243572856685003200955151449727786123781385728108815940504735383413506758523033251327474485528127077834540055270215549605908906262509468579754951353763978659990673026191308819763698496328049297079965961031433725046504598407545
dQ=807539273863108018516295891953051484643110138565773549272017951539045988986311941686270708518515467401470853102117090593288730727113473781024432704560030983108790052339640179712790080208743944269054840273805706936788897052967506593
qInv=605072335571217146316673658160761917910412905765314189108004571745387224528957349349096131343437305686727527738046406160698020069593830061387522565814243467840337599694881465305415514544578066624881549000875583052614286821007114745
s1=366478150883847870448379626688961621210409402704492498417807616987386952154742999158611661095423664280214837124543491225036519028191628796734725958785229271484883072038387215541775577145647449293452446326624765318698143729176504634
s2=57157570705178137112627062160203855130811408135508235599470349106409594425416446377740187864095988477422179138305176205401737382767316291629594752287917740769024465346317740540556636293566855384291783008629989264065624204367187803
s_crt=194858108494819440098685122478321316014401467520388897494523722359964950819000865198278598326556338441731291390978207309230018343521359160497581733617474249968667342584696269639180575180958583580722050351138469438960348833767744629570681596174884405176333577765728612398811644545417428572898447196363423840861913767912497435252328696104666673865295834446450914138374593320878736661785601657329954889591328459344223329354691434003171605206173729521966475424443521
== Signature using (d,N)) ===
s_d=194858108494819440098685122478321316014401467520388897494523722359964950819000865198278598326556338441731291390978207309230018343521359160497581733617474249968667342584696269639180575180958583580722050351138469438960348833767744629570681596174884405176333577765728612398811644545417428572898447196363423840861913767912497435252328696104666673865295834446450914138374593320878736661785601657329954889591328459344223329354691434003171605206173729521966475424443521

The signatures are the same!!!
Time with CRT = 0.01563405990600586 Seconds
Time Traditional = 0.04686307907104492 Seconds

We can see that with CRT the signature time took around 15.6ms, while with the traditional method it was around 46.9ms. In this case, the CRT signature method is over three times faster than the traditional method.

Conclusions

So, with a less complex operation, we can see that the CRT method can be many times faster than the traditional signing method, but still, give the same result. In our case, the CRT method is over three times faster. Go try here:

https://asecuritysite.com/rsa/rsa_crt4

So, RSA is still alive in the world of signing. While ECDSA is King of Bitcoin and Ethereum, the humble RSA signing method is still the most popular in actually defining the trust infrastructure of the Internet. So, after over four decades, RSA is still alive and kicking. It’s just that quantum computers are on our horizon, so it will have to leave some time in the next two decades. But, it has served us well and secured the Internet. With CRT, it addresses some of its weaknesses, and where we can create signatures with reasonable processing requirements.